小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?
(成本=进价×销售量)
(本题10分)为美化萧山,创建文明城市.园林部门决定利用现有的3600盆甲种花卉和2900盆 乙种花卉搭配A、B两种园艺造型共50个,
乙种花卉搭配A、B两种园艺造型共50个, 摆放在人民广场两侧,搭配每个造型所需花卉情况如下表所示
摆放在人民广场两侧,搭配每个造型所需花卉情况如下表所示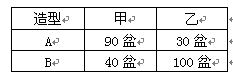
综合上述信息,解答下列问题:(1)符合题意的搭配方案有哪几种?
(2)若搭配一个A型造型的成本为1000元,
搭配一个B型造型的成本为1200元.试说明运用(1)中哪种方案成本最低?
(本题8分)
某校八年级200名女生在体育测试中进行了立定跳远的测试.现从200名女生中随机抽取10名女生进行测试,下面是她们测试结果的条形统计图.(另附某校八年级女生立定跳远的计分标准)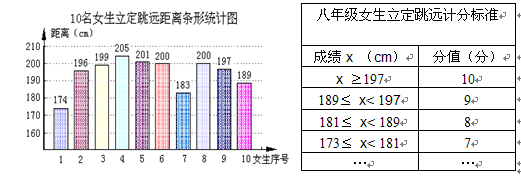
(1)求这10名女生立定跳远距离的中位数,立定跳远得分的众数和平均数.
(2)请你估计该校200名女生在立定跳远测试中得10分的人数.
(本小题满分8分)已知y – 2与x成正比例关系,且当x=1时,y=5.
(1)求
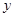 与
与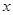 之间的函数解析式;
之间的函数解析式;(2)画出这个函数的图像,并求出该图像与坐标轴围成的三角形的面积。.
(本题6分)在平面直角坐标系中, △ABC的三个顶点的位置如图所示,点A'的坐标是(-2,2), 现将△ABC平移,使点A变换为点A',点B′、C′分别是B、C的对应点.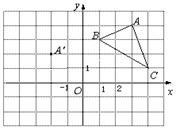
(1)请画出平移后的像△A'B'C'(不写画法) ,
并直接写出点B′、C′的坐标:
B′() 、C′ () ;(2)若△ABC 内部一点P的坐标为(a,b),则点P
的对应点P ′的坐标是 () .
(本题6分)如图,是一个无盖立方体盒子,请把下列不完整的展开图补充完整。(请画出三种)