已知无穷数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,其中
,其中 、
、 、
、 是常数.
是常数.
(1)若 ,
, ,
, ,求数列
,求数列 的通项公式;
的通项公式;
(2)若 ,
, ,
, ,且
,且 ,求数列
,求数列 的前
的前 项和
项和 ;
;
(3)试探究 、
、 、
、 满足什么条件时,数列
满足什么条件时,数列 是公比不为
是公比不为 的等比数列.
的等比数列.
(本小题共10分)甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约 。甲表示只要面试合格就签约,乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约,设每人面试合格的概率都是
。甲表示只要面试合格就签约,乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约,设每人面试合格的概率都是 ,且面试是否合格互不影响,求:
,且面试是否合格互不影响,求:
①至少有1人面试合格的概率;
②签约人 数ξ的分布列和数学期望。
数ξ的分布列和数学期望。
(本小题共10分) 已知集合A=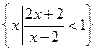 ,
, B=
B=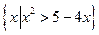 ,C=
,C=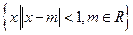
①求A∩B;
②若(A∩B)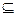 C,求m的取值范围。
C,求m的取值范围。
(本小题满分14分)
已知曲线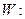
 经过点A(2,1),过A作倾斜角互补的两条不同直线
经过点A(2,1),过A作倾斜角互补的两条不同直线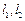 .
.
(Ⅰ)求抛物线 的方程及准线方程;
的方程及准线方程;
(Ⅱ)当直线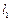 与抛物线
与抛物线 相切时,求直线
相切时,求直线 与抛物线
与抛物线 所围成封闭区域的面积;
所围成封闭区域的面积;
(Ⅲ)设直线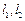 分别交抛物线
分别交抛物线 于B,C两点(均不与A重合),若以线段BC为直径的圆与抛物线
于B,C两点(均不与A重合),若以线段BC为直径的圆与抛物线 的准线相切,求直线BC的方程.
的准线相切,求直线BC的方程.
(本小题满分12分)
已知函数 ,其中
,其中 为实常数。
为实常数。
(1)当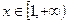 时,
时,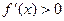 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(2)求函数 的单调区间。
的单调区间。
(本小题满分12分)
在数列{an}中,a1=1,当n≥2时,an,Sn,Sn- 成等比数列
成等比数列
(1)求a2,a3,a4,并推出an的表达式;
(2)用数学归纳法证明所得的结论;