某产品具有一定的时效性,在这个时效期内,由市场调查可知,在不做广告宣传且每件获利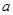 元的前提下,可卖出
元的前提下,可卖出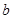 件;若做广告宣传,广告费为
件;若做广告宣传,广告费为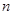 千元比广告费为
千元比广告费为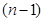 千元时多卖出
千元时多卖出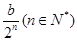 件.
件.
(Ⅰ)试写出销售量 与
与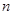 的函数关系式;
的函数关系式;
(Ⅱ)当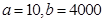 时,厂家应生产多少件这种产品,做几千元的广告,才能获利最大?
时,厂家应生产多少件这种产品,做几千元的广告,才能获利最大?
(本小题满分12分)
设数列 的前
的前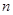 项和为
项和为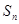 ,且
,且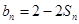 ;数列
;数列 为等差数列,且
为等差数列,且
(1)求数列 的通项公式;
的通项公式;
(2)若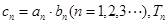 为数列
为数列 的前
的前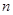 项和,求证:
项和,求证:
(本小题满分12分)
已知 的内角为A、B、C的对边分别为
的内角为A、B、C的对边分别为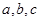 ,B为锐角,向量
,B为锐角,向量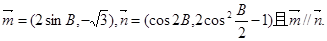
(1)求B的大小;
(2)如果 ,求
,求 的最大值.
的最大值.
已知函数
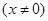 只有一个零点
只有一个零点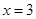 .
.
(Ⅰ)求函数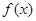 的解析式;
的解析式;
(Ⅱ)若函数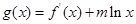 在区间
在区间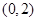 上有极值点,求
上有极值点,求 取值范围;
取值范围;
(Ⅲ)是否存在两个不等正数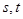
 ,当
,当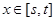 时,函数
时,函数 的值域也是
的值域也是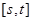 ,若存在,求出所有这样的正数
,若存在,求出所有这样的正数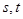 ;若不存在,请说明理由;
;若不存在,请说明理由;
(本小题满分12分)
已知椭圆 的左、右焦点为
的左、右焦点为 、
、 ,上顶点为A,直线
,上顶点为A,直线 交椭圆于
交椭圆于 . 如图所示沿
. 如图所示沿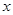 轴折起,使得平面
轴折起,使得平面 平面
平面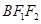 . 点
. 点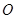 为坐标原点.
为坐标原点.
( I ) 求三棱锥 的体积;
的体积;
(Ⅱ)线段 上是否存在点
上是否存在点 ,使得
,使得 ,若存在,请在图1中指出点
,若存在,请在图1中指出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分12分)
如图,从点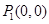 做x轴的垂线交曲线
做x轴的垂线交曲线 于点
于点 曲线在
曲线在 点处的切线与x轴交于点
点处的切线与x轴交于点 ,再从
,再从 做x轴的垂线交曲线于点
做x轴的垂线交曲线于点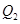 ,依次重复上述过程得到一系列点:
,依次重复上述过程得到一系列点: 记
记
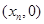 ,
, .
.
(Ⅰ)求点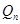 处的切线方程,并指出
处的切线方程,并指出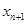 与
与 的关系;
的关系;
(Ⅱ)求