如图，在直三棱柱ABC—A1B1C1中，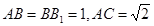 
，直线B1C与平面ABC成45°角.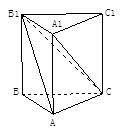
（1）求证：平面A1B1C⊥平面B1BCC1；
（2）求二面角A—B1C—B的余弦值.
如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB.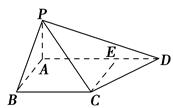 
(1)求证：CE⊥平面PAD；
(2)若PA＝AB＝1，AD＝3，CD＝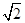
，∠CDA＝45°，求四棱锥P-ABCD的体积．
已知Sn是数列{an}的前n项和，且an＝Sn－1＋2(n≥2)，a1＝2.
(1)求数列{an}的通项公式．
(2)设bn＝
，Tn＝bn＋1＋bn＋2＋…＋b2n，是否存在最大的正整数k，使得
对于任意的正整数n，有Tn＞
恒成立？若存在，求出k的值；若不存在，说明理由．
已知等差数列{an}的前n项和为Sn，n∈N*，且a2＝3，点(10，S10)在直线y＝10x上．
(1)求数列{an}的通项公式；
(2)设bn＝2an＋2n，求数列{bn}的前n项和Tn.
设数列{an}的前n项和为Sn，已知ban－2n＝(b－1)Sn.
(1)证明：当b＝2时，{an－n·2n－1}是等比数列；
(2)求{an}的通项公式．
在等差数列{an}中，a16＋a17＋a18＝a9＝－36，其前n项和为Sn.
(1)求Sn的最小值，并求出Sn取最小值时n的值；
(2)求Tn＝|a1|＋|a2|＋…＋|an|.