(本小题满分12分)如图所示,矩形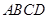 的对角线交于点G,AD⊥平面
的对角线交于点G,AD⊥平面 ,
, ,
,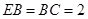 ,
, 为
为 上的点,且BF⊥平面ACE
上的点,且BF⊥平面ACE
(1)求证: 平面
平面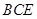 ;
;
(2)求三棱锥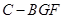 的体积.
的体积.
(本小题满分12分)
甲乙两奥运会主办城市之间有7条网线并联,这7条网线能通过的信息量分别为1,1,2,2,2,3,3,现从中任选三条网线,设可通过的信息量为X,当可通过的信息最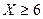 ,则可保证信息通畅。
,则可保证信息通畅。
(I)求线路信息通畅的概率;
(II)求线路可通过的信息量X的分布列及数学期望。
(本小题满分14分)
已知函数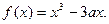
(I)当a= 1时,求函数
1时,求函数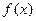 的单调区间;
的单调区间;
(II)求函数 在区间[0,1]上的最小值。
在区间[0,1]上的最小值。
(本小题满分12分)
某旅游公司为 3个旅游团提供甲、乙、丙、丁4条旅游线路,每个旅游团从中任选一条。
3个旅游团提供甲、乙、丙、丁4条旅游线路,每个旅游团从中任选一条。
(I)求3个旅游团选择3条不同的旅游线路的概率;
(II)求恰有2条旅游线路没有被选择的概率;
(III)求选择甲旅游线路的旅游团数的分布列及数学期望。
(本小题满分8分)
已知直线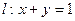 与椭圆
与椭圆 (
( 为参数),若直线
为参数),若直线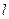 与椭圆交于A,B两点,求线段AB的长度。
与椭圆交于A,B两点,求线段AB的长度。
(满分10分)已知数列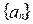 ,
,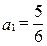 ,若以
,若以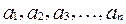 为系数的二次方程
为系数的二次方程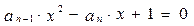 都有根
都有根 ,且满足
,且满足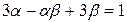 。
。
(1)求数列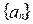 通项公式;
通项公式;
(2)求数列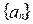 前
前 项和
项和 .
.