有两个直角三角形,在△ABC中,∠ACB=90°,AC=3,BC=6,在△DEF中,∠FDE=90°,DE=DF=4。将这两个直角三角形按图1所示位置摆放,其中直角边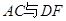 在同一直线
在同一直线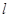 上,且点
上,且点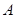 与点
与点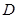 重合。现固定
重合。现固定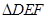 ,将
,将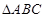 以每秒1个单位长度的速度在
以每秒1个单位长度的速度在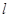 上向右平移,当点
上向右平移,当点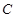 与点
与点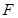 重合时运动停止。设平移时间为
重合时运动停止。设平移时间为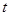 秒。
秒。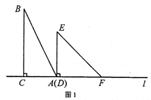
(1)当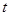 为 秒时,
为 秒时,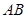 边恰好经过点
边恰好经过点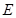 ;当
;当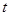 为 秒时,运动停止;
为 秒时,运动停止;
(2)在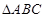 平移过程中,设
平移过程中,设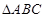 与
与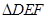 重叠部分的面积为
重叠部分的面积为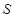 ,请直接写出
,请直接写出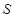 与
与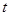 的函数关系式,并写出
的函数关系式,并写出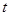 的取值范围;
的取值范围;
(3)当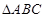 停止运动后,如图2,
停止运动后,如图2,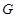 为线段
为线段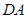 上一点,若一动点
上一点,若一动点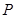 从点
从点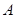 出发,先沿
出发,先沿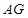 方向运动,到达点
方向运动,到达点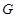 后再沿斜坡
后再沿斜坡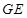 方向运动到达点
方向运动到达点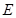 ,若该动点
,若该动点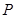 在线段
在线段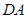 上运动的速度是它在斜坡
上运动的速度是它在斜坡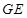 上运动速度的2倍,试确定斜坡
上运动速度的2倍,试确定斜坡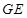 的坡度,使得该动点从点
的坡度,使得该动点从点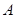 运动到点
运动到点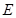 所用的时间最短。(要求,简述确定点
所用的时间最短。(要求,简述确定点 位置的方法,但不要求证明。)
位置的方法,但不要求证明。)
已知⊙O的半径为13cm,弦AB∥CD,AB=24cm,CD=10cm,求AB和CD之间的距离.
已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,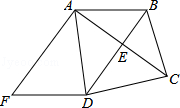
(1)证明四边形ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.
如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
前夕,某商店根据市场调查,用3000元购进第一批盒装花,上市后很快售完,接着又用5000元购进第二批这种盒装花.已知第二批所购花的盒数是第一批所购花盒数的2倍,且每盒花的进价比第一批的进价少5元.求第一批盒装花每盒的进价是多少元?
因式分解:
(1)4a2b2﹣(a2+b2)2;
(2)(a+x)4﹣(a﹣x)4.
(3)分解因式:(x﹣y)2﹣4(x﹣y﹣1)
(4)a2﹣4ax+4a;
(5)(x2﹣1)2+6(1﹣x2)+9.