某人定制了一批地砖,每块地砖(如图(1)所示)是边长为0.5米的正方形ABCD.点E、F分别在边BC和CD上,△CFE、△ABE和四边形AEFD均由单一材料制成,制成△CFE、△ABE和四边形AEFD的三种材料的价格依次为每平方米30元、20元、10元.若将此种地砖按图(2)所示的形式铺设,则中间的阴影部分组成正方形EFGH.已知烧制该种地砖平均每块需加工费0.35元,要使BE长尽可能小,且每块地砖的成本价为4元(成本价=材料费用+加工费用),则CE长应为多少米?
解:设 CE=x,则S△CFE= ,S△ABE=
S四边形AEFD= (用含x的代数式表示,不需要化简)。
由题意可得:(请你继续完成未完成的部分)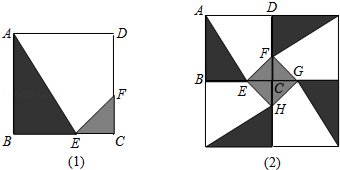
先化简: ,然后解答下列问题:
,然后解答下列问题:
(1)当 时,求原代数式的值;
时,求原代数式的值;
(2)原代数式的值能等于 吗?为什么?
吗?为什么?
如图,在Rt△ABC中,∠ACB=900,AC=6,BC=8.动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM、PN,当点N运动到点A时,M、N两点同时停止运动,设运动时间为t秒.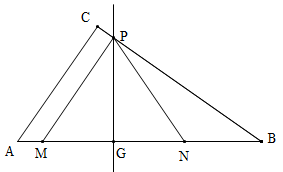
(1)当t=秒时,动点M、N相遇;
(2)设△PMN的面积为S,求S与t之间的函数关系式;
(3)取线段PM的中点K,连接KA、KC,在整个运动过程中,△KAC的面积是否变化?若变化,直接写出它的最大值和最小值;若不变化,请说明理由.
阅读理解:
如图①,如果四边形ABCD满足AB=AD,CB=CD,∠B=∠D=90°,那么我们把这样的四边形叫做“完美筝形”.
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状,再展开得到图③,其中CE,CF为折痕,∠BCE=∠ECF=∠FCD,点B′为点B的对应点,点D′为点D的对应点,连接EB′,FD′相交于点O.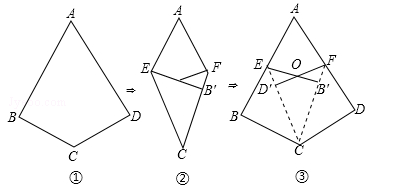
简单应用:
(1)在平行四边形、矩形、菱形、正方形四种图形中,一定为“完美筝形”的是;
(2)当图③中的∠BCD=120°时,∠AEB′=°;
(3)当图②中的四边形AECF为菱形时,对应图③中的“完美筝形”有个(包含四边形ABCD).
拓展提升:
(4)当图③中的∠BCD=90°时,连接AB′,请探求∠AB′E的度数,并说明理由.
小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.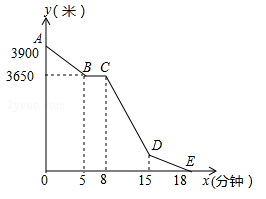
(1)求小丽步行的速度及学校与公交站台乙之间的距离;
(2)当8≤x≤15时,求y与x之间的函数关系式.
如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF.
(1)直接写出点F的坐标;
(2)求线段OB的长及图中阴影部分的面积.