在重阳节敬老爱老活动中,某校计划组织志愿者服务小组到“夕阳红”敬老院为老人服务,准备从初三(1)班中的3名男生小亮、小明、小伟和2名女生小丽、小敏中选取一名男生和一名女生参加学校志愿者服务小组.
(1)若随机选取一名男生和一名女生参加志愿者服务小组,请用树状图或列表法写出所有可能出现的结果;
(2)求出恰好选中男生小明与女生小丽的概率.
【改编】如图,己知:反比例函数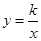 的图象与一次函数y=mx+b的图象交于点A(1,4),点B(-4,n).
的图象与一次函数y=mx+b的图象交于点A(1,4),点B(-4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积.
(3)在直线AB上是否存在点P,使得△AOP是以OP为腰的等腰三角形,若存在,直接写出点P的坐标,若不存在,说明理由.
如图,已知△ABC的三个顶点的坐标分别 为A(-6,0)、B(-2,3)、C(-1,0).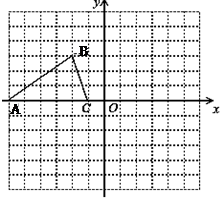
(1)将△ABC绕坐标原点O逆时针旋转90°.画出对应的△A′B′C′图形;
(2)若四边形A′B′C′D′为平行四边形,请直接写出第四个顶点D′的坐标.
先化简,再求值: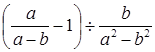 ,其中a=
,其中a=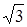 +1,b=
+1,b=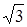 -1.
-1.
已知二次函数的图象经过点(0,3),顶点坐标为(1,4),
(1)求这个二次函数的解析式;
(2)求图象与x轴交点A、B两点的坐标;
(3)图象与y轴交点为点C,求三角形ABC的面积.
【改编】如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).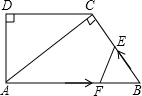
(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y关于t的函数关系式,并求出y的最小值.