某景点的门票价格规定如下表
| 购票人数 |
1—50人 |
51—100人 |
100人以上 |
| 每人门票价 |
12元 |
10元 |
8元 |
某校八年(一)、(二)两班共100多人去游览该景点,其中(一)班不足50人,(二)班多于50人,如果两班都以班为单位分别购票,则一共付款1126元.如果以团体购票,则需要付费824元,问:
(1)两班各有多少名学生?
(2)如果你是学校负责人,你将如何购票?你的购票方法可节省多少钱?
x(x-3)=15-5x
如图,在 中,
中, ,
, 于
于 ,若
,若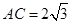 ,
,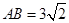 ,则
,则 为
为
已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,如图①∠EDF的两边分别交AC、CB(或它们的延长线)于E、F.当∠EDF的边DE⊥AC于E时, ,
, ,
, 满足
满足 ;
;
(1)如图②,当∠EDF的边DE和AC不垂直时,请证明上述结论仍然成立;
(2)如图③,当∠EDF的边DE与AC的延长线交于点E的情况下,上述结论是否成立?若成立,请给予证明;若不成立, ,
, ,
, 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
如图(1),在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是 ,位置关系是 ;[www.z@zs^te%#p.com~]
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点,点P从点A出发向点B运动,点Q从点B出发向点C运动,它们同时出发,且速度都是1cm/s.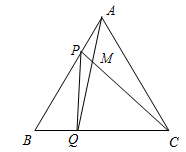
(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;
(2)何时△PBQ是直角三角形?