如图(1),在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(1)请判断:AF与BE的数量关系是 ,位置关系是 ;[www.z@zs^te%#p.com~]
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.

如图,在平面直角坐标系中,二次函数 交 轴于点 、 ,交 轴于点 ,在 轴上有一点 ,连接 .
(1)求二次函数的表达式;
(2)若点 为抛物线在 轴负半轴上方的一个动点,求 面积的最大值;
(3)抛物线对称轴上是否存在点 ,使 为等腰三角形?若存在,请直接写出所有 点的坐标,若不存在,请说明理由.

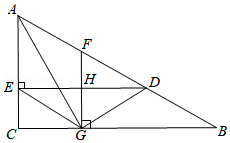
如图, 中, 是 上一点, 于点 , 是 的中点, 于点 ,与 交于点 ,若 , 平分 ,连接 , .
(1)求证: ;
(2)小亮同学经过探究发现: .请你帮助小亮同学证明这一结论.
(3)若 ,判定四边形 是否为菱形,并说明理由.
如图,矩形 的两边 、 的长分别为3、8, 是 的中点,反比例函数 的图象经过点 ,与 交于点 .
(1)若点 坐标为 ,求 的值及图象经过 、 两点的一次函数的表达式;
(2)若 ,求反比例函数的表达式.

为增强学生的安全意识,我市某中学组织初三年级1000名学生参加了“校园安全知识竞赛”,随机抽取一个班学生的成绩进行整理,分为 , , , 四个等级,并把结果整理绘制成条形统计图与扇形统计图(部分),请依据如图提供的信息,完成下列问题:
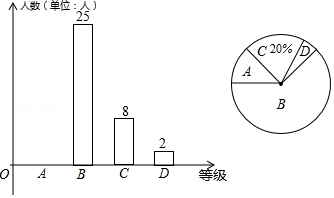
(1)请估计本校初三年级等级为 的学生人数;
(2)学校决定从得满分的3名女生和2名男生中随机抽取3人参加市级比赛,请求出恰好抽到2名女生和1名男生的概率.
文美书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、14元,甲种图书每本的售价是乙种图书每本售价的1.4倍,若用1680元在文美书店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.
(1)甲乙两种图书的售价分别为每本多少元?
(2)书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完.