已知向量
(1)若 为
为 的中点,
的中点, ,求
,求 的值;
的值;
(2)若 是以
是以 为斜边的直角三角形,求
为斜边的直角三角形,求 的值.
的值.
(本小题满分12分)甲乙两人进行围棋比赛,约定每局胜者得1分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时停止.设甲在每局中获胜的概率
局时停止.设甲在每局中获胜的概率
 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为 .
.
(1)求 的值;
的值;
(2)设 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量 的分布列和数学期望
的分布列和数学期望 .
.
(本题满12分)在 中,角
中,角 的对边分别为
的对边分别为 且
且
(1)求 的值;
的值;
(2)若 ,且
,且 ,求
,求 的值.
的值.
已知函数 .
.
(Ⅰ)设a=1,b=-1,求f(x)的单调区间;
(Ⅱ)若对任意x>0,f(x)≥f(1).试比较lna与-2b的大小.
已知椭圆 :
: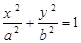 (
( )过点(2,0),且椭圆C的离心率为
)过点(2,0),且椭圆C的离心率为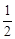 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若动点 在直线
在直线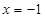 上,过
上,过 作直线交椭圆
作直线交椭圆 于
于 两点,且
两点,且 为线段
为线段 中点,再过
中点,再过 作直线
作直线 .求直线
.求直线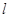 是否恒过定点,若果是则求出该定点的坐标,不是请说明理由。
是否恒过定点,若果是则求出该定点的坐标,不是请说明理由。
在 中,内角
中,内角 所对的边分别为
所对的边分别为 ,
, .
.
(Ⅰ)确定角 的大小;
的大小;
(Ⅱ)若 的角平分线
的角平分线 交线段
交线段 于
于 ,且
,且 ,设
,设 .
.
(ⅰ)试确定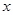 与
与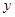 的关系式;
的关系式;
(ⅱ)记 和
和 的面积分别为
的面积分别为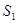 、
、 ,问当
,问当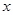 取何值时,
取何值时, +
+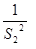 的值最小,最小值是多少?
的值最小,最小值是多少?