为了探究动能定理,一位同学设计了如图所示的实验装置。他先固定并调整斜槽,让末端O点的切线水平,再将一木板竖直放置并固定,木板到斜槽末端O的距离为s,使小球从斜槽上某一标记点由静止释放,若小球到达斜槽底端时下落的高度为H、小球从O点做平抛运动击中木板时下落的高度为y。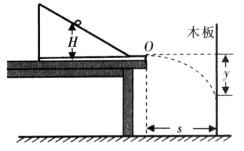
(1)假定斜槽光滑,小球由静止滑下到击中木板的过程中,满足动能定理的关系式为:__________。
(2)若斜槽倾角为θ,小球与斜槽之间的动摩擦因数为μ(只考虑滑动摩擦力,且小球与水平槽之间的摩擦不计),小球由静止滑下到击中木板的过程中,满足动能定理的关系式是:___________。
(3)改变小球在斜槽上的释放位置,进行多次测量,能得到多组关于H和y的数据,若以H为横坐标,从(1)、(2)中的关系式可知以________为纵坐标,通过描点作图,能得到一条倾斜的直线。
如图甲为“用DIS(位移传感器、数据采集器、计算机)“研究加速度和力的关系”的实验装置。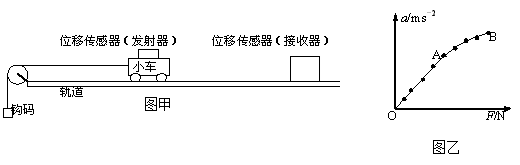 22
22
(1)在该实验中必须采用控制变量法,应保持___________不变,用钩码所受的重力作为小车所受外力,用DIS测小车的加速度.。
(2)改变所挂钩码的数量,多次重复测量。在某次实验中根据测得的多组数据可画出a-F关系图线(如图乙所示)。
①分析此图线的OA段可得出的实验结论是_________________________________。
②此图线的AB段明显偏离直线,造成此误差的主要原因是()
| A.小车与轨道之间存在摩擦 | B.导轨保持了水平状态 |
| C.所挂钩码的总质量太大 | D.所用小车的质量太大 |
(1)如图甲是测量滑块与木板间动摩擦因数的装置,将木板水平固定在桌面上,利用一根压缩的短弹簧来弹开滑块.请完成下列实验操作与分析: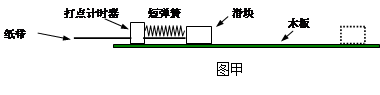
①先接通打点计时器的电源,再释放滑块,滑块被弹开后继续拖动纸带运动一段距离后停下.
②某次实验打出的纸带后面的一段如图乙,其中B点为滑块停下时在纸带上记录到的点.打点计时器打点周期为T,其他数据已在图中标出,则滑块通过A点的速度v= (用T、x1、x2表示);再用 测出AB之间的距离L.
③已知重力加速度为g,则滑块与木板间动摩擦因数µ= (用g、L、T、x1、x2表示).由于纸带与计时器存在阻力,测出的动摩擦因数µ与真实值相比 (填“一样大”、“偏大”或“偏小”). (2)某同学用“伏安法”测一只阻值约十几kΩ的电阻R的阻值,所用的器材有:内阻约100kΩ、量程为0-15V的电压表V,内阻约100Ω、量程为1mA的电流表 ,最大电阻为50Ω的滑动变阻器,电源,电键和导线若干.
(2)某同学用“伏安法”测一只阻值约十几kΩ的电阻R的阻值,所用的器材有:内阻约100kΩ、量程为0-15V的电压表V,内阻约100Ω、量程为1mA的电流表 ,最大电阻为50Ω的滑动变阻器,电源,电键和导线若干.
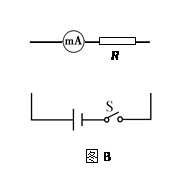
①若先用表盘如图A的多用表的欧姆挡粗测其电阻,则应将选择开关旋到“ ”挡
(选填×10Ω、×100Ω或×1kΩ).
②请将图B中用“伏安法”测量该电阻的电路图补充完整.
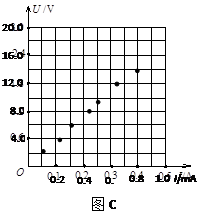
③由实验测得的7组数据已在图C的U-I图上标出,请你完成图线,并由图线求出R="_______" Ω. (结果保留三位有效数字)
I.某同学利用如图(a)装置做“探究弹簧弹力大小与其长度的关系”的实验。
①在安装刻度尺时,必须使刻度尺保持 状态。
②他通过实验得到如图(b)所示的弹力大小F与弹簧长度x的关系图线。由此图线可得该弹簧的原长x0= cm,劲度系数k=N/m。
③他又利用本实验原理把该弹簧做成一把弹簧秤,当弹簧秤上的示数如图(c)所示时,该弹簧的长度x= cm。
Ⅱ.某学习小组为探究导电溶液的电阻在体积相同时,电阻值与长度的关系。选取一根乳胶管,里面灌满了盐水,两端用粗铜丝塞住管口,形成一段封闭的盐水柱。进行了如下实验:
(1)该小组将盐水柱作为纯电阻,粗测其电阻约为几千欧。现采用伏安法测盐水柱的电阻,有如下实验器材可供选择:
| A.直流电源:电动势12V,内阻很小,额定电流1A; |
B.电流表A1:量程0~10mA,内阻约 ; ; |
C.电流表A2:量程0~600mA,内阻约 ; ; |
D.电压表V:量程0~15V,内阻约 ; ; |
E.滑动变阻器R1:最大阻值 ;
;
F.滑动变阻器R2:最大阻值 ;
;
G.开关.导线等
在可供选择的器材中,应选用的电流表是_______(填“A1”或“A2”),应该选用的滑动变阻器是________(填“R1”或“R2”)。
(2)根据所选的器材在题给的方框内画出实验的电路图。
(3)握住乳胶管两端把它均匀拉长,多次实验测得盐水柱长度L,电阻R的数据如下表:
| 实验次数 |
1 |
2 |
3 |
4 |
5 |
6 |
| 长度L(cm) |
20.0 |
25.0 |
30.0 |
35.0 |
40.0 |
45.0 |
电阻R( ) ) |
1.3 |
2.1 |
3.0 |
4.1 |
5.3 |
6.7 |
为了研究电阻R与长度L的关系,该小组用纵坐标表示电阻R,作出了如图所示的图线,你认为横坐标表示的物理量是____________。
在做“用单摆测定重力加速度”的实验中,某同学先测得摆线长为89.2 cm,用20分度的游标卡尺测得摆球的直径示数如图所示,然后用秒表记录了单摆做30次全振动的时间。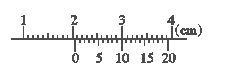
(1)该单摆的摆长为 cm。
(2)如果该同学测得的g值偏大,可能的原因是( )
| A.记录摆长时误将摆球的直径作为半径 |
| B.开始计时时,秒表过迟按下 |
| C.摆线上端牢固地系于悬点,摆动中出现松动,使摆线长度增加了 |
| D.实验中误将29次全振动数为30次 |
(3)为了提高实验精度,在实验中可改变几次摆长l,测出相应的周期T,从而得出一组对应的l与T的数值,再以l为横坐标,T2为纵坐标,将所得数据连成直线如图所示,则测得的重力加速度g= m/s2。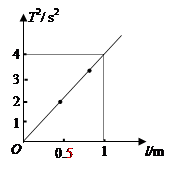
在研究电磁感应现象的实验中所用的器材如图所示。它们是:①电流计、②直流电源、③带铁芯的线圈A、④线圈B、⑤电键、⑥滑动变阻器(用来控制电流以改变磁场强弱)。
(1) 试按实验的要求在实物图上连线(图中已连好一根导线)。
(2) 若连接滑动变阻器的两根导线接在接线柱C和D上,而在电键刚闭合时电流表指针右偏,则电键闭合后滑动变阻器的滑动触头向接线柱C移动时,电流计指针将__________(填“左偏”、“右偏”、“不偏”)。