如图①,正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A⇒B⇒C⇒D匀速运动,同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,设运动的时间为t秒.
(1)当P点在边AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)如果点P、Q保持原速度不变,当点P沿A⇒B⇒C⇒D匀速运动时,OP与PQ能否相等?若能,求出所有符合条件的t的值;若不能,请说明理由.
如图,在笔直的公路L的同侧有A、B两个村庄,已知A、B两村分别到公路的距离AC=3km,BD=4km。现要在公路上建一个汽车站P,使该车站到A、B两村的距离相等,
(1)试用直尺和圆规在图中作出点P;(保留作图痕迹)
(2)若连接AP、BP,测得∠APB=90°,求A村到车站的距离
如图所示,四边形ABCD中,AB=4,BC=3,AD=13,CD=12,∠B=90°,求该四边形的面积.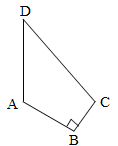
已知:如图,在△BAC中,AB=AC,,D,E分别为AB,AC边上的点,且DE∥BC,求证: △ADE是等腰三角形. 
已知:如图,点B、F、C、E在一条直线上,∠B=∠E,∠ACB=∠DFE,且BF=EC.求证:△ABC≌△DEF.
先化简,再求值:(a-2b)2-4b( a+b),其中a=-1,b=2.
a+b),其中a=-1,b=2.