在长方体ABCD-A1B1C1D1中,AD=1,AA1=AB=2.点E是线段AB上的动点,点M为D1C的中点.
(1)当E点是AB中点时,求证:直线ME‖平面ADD1 A1;
(2)若二面角AD1EC的余弦值为 .求线段AE的长.
.求线段AE的长.
(本小题满分12分)数列{an}中,a1=1,n≥2时,其前n项的和Sn满足Sn2=an(Sn- ).
).
(1)求Sn的表达式;
(2)设bn= ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
(本小题满分12分)在△ABC中,a、b、c分别是角A、B、C的对边,且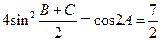 ,
,
(1)求∠A的度数;
(2)若a=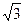 ,b+c=3,求b和c的值.
,b+c=3,求b和c的值.
已知数列 中,
中, 且点
且点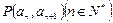 在直线
在直线 上.
上.
(1)求数列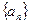 的通项公式;
的通项公式;
(2)若函数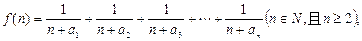 求函数
求函数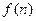 的最小值;
的最小值;
(3)设 表示数列
表示数列 的前n项和.试问:是否存在关于
的前n项和.试问:是否存在关于 的整式
的整式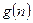 ,使得
,使得 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立? 若存在,写出
恒成立? 若存在,写出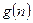 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
(本小题满分12分)如图,已知直线l: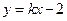 与抛物线C:
与抛物线C: 交于A,B两点,
交于A,B两点,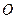 为坐标原点,
为坐标原点,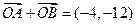 。
。
(Ⅰ)求直线l和抛物线C的方程;
(Ⅱ)抛物线上一动点P从A到B运动时,
求△ABP面积最大值.
(本小题满分12分)聊城市政府要用三辆汽车从新市政府把工作人员接到老市政府,已知从新市政府到老市政府有两条公路,汽车走公路①堵车的概率为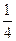 ,不堵车的概率为
,不堵车的概率为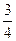 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为 ,不堵车的概率为
,不堵车的概率为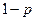 .若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
.若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响.
(1)若三辆汽车中恰有一辆汽车被堵的概率为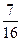 ,求走公路②堵车的概率;
,求走公路②堵车的概率;
(2)在(1)的条件下,求三辆汽车中被堵车辆的个数 的分布列和数学期望.
的分布列和数学期望.