(本小题满分7分)选修4-2:矩阵与变换
二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换成点(-1,-1)与(0,-2).
(Ⅰ)求矩阵M;
(Ⅱ)设直线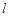 在变换M作用下得到了直线m:2x-y=4,求
在变换M作用下得到了直线m:2x-y=4,求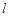 的方程
的方程
(本小题满分14分)已知函数 (
(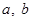 为实数,
为实数, ,
,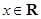 ),
),
(Ⅰ)若 ,且函数
,且函数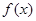 的值域为
的值域为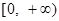 ,求
,求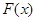 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当 时,
时,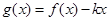 是单调函数,求实数
是单调函数,求实数 的取值范围;
的取值范围;
(Ⅲ)设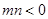 ,
,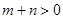 ,
, ,且函数
,且函数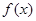 为偶函数,判断
为偶函数,判断 是否大于
是否大于 ?
?
(本小题满分13分)已知函数 。
。
(Ⅰ)当 时,求曲线
时,求曲线 在
在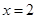 处切线的斜率;
处切线的斜率;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)当 时,求
时,求 在区间
在区间 上的最小值。
上的最小值。
(本小题满分13分)某单位有员工1000名,平均每人每年创造利润10万元。为了增加企业竞争力,决定优化产业结构,调整出 名员工从事第三产业,调整后他们平均每人每年创造利润为
名员工从事第三产业,调整后他们平均每人每年创造利润为 万元
万元 ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高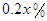 .
.
(Ⅰ)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(Ⅱ)在(Ⅰ)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则 的取值范围是多少?
的取值范围是多少?
(本小题满分13分)已知函数 ,其中
,其中 为常数,且
为常数,且 是函数
是函数 的一个零点。
的一个零点。
(Ⅰ)求函数 的最小正周期和所有对称轴方程;
的最小正周期和所有对称轴方程;
(Ⅱ)当 时,求函数
时,求函数 的值域。
的值域。