阅读理解:
如图1,若在四边形ABCD的边AB上任取一点E(点E与点A,B不重合),分别连结ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,若∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,请直接写出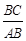 的值.
的值.
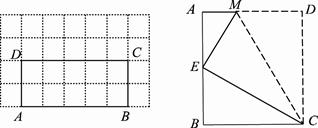
图1 图2 图3
图(a)、图(b)是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.请在图(a)、图(b)中,分别画出符合要求的图形,所画图形各顶点必须与方格纸中的小正方形顶点重合.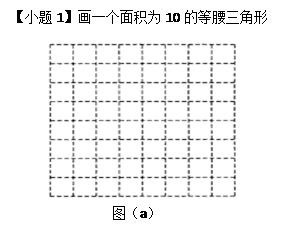

.已知a=(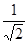 )
) ,b="2cos" 45
,b="2cos" 45 -
- ,c=(2011-
,c=(2011-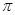 )
)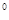 ,d=
,d=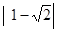
请化简这四个数;
从这四个数中任取两个,积为无理数的概率是多少。
已知:把Rt△ABC和Rt△DEF按如图甲摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠BAC = ∠DEF = 90°,∠ABC = 45°,BC =" 9" cm,DE =" 6" cm,EF =" 8" cm.
如图乙,△DEF从图甲的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△DEF的顶点F出发,以3 cm/s的速度沿FD向点D匀速移动.当点P移动到点D时,P点停止移动,△DEF也随之停止移动.DE与AC相交于点Q,连接BQ、PQ,设移动时间为t(s).解答下列问题:设三角形BQE的面积为y(cm2),求y与t之间的函数关系式,并写出自变量t的取值范围;
当t为何值时,三角形DPQ为等腰三角形?
是否存在某一时刻t,使P、Q、B三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由


按右图的流程,输入一个数据x,根据y与x的函数关系式就 输出一个数据y,这样可以将一组数据变换成另一组新的数据,要使任意一组都在20到100(含20和100)之间的数据,变换成一组新数据后能满足下列两个要求:
(ⅰ)、新数据都在60到100(含60和100)之间。
(ⅱ)、新数据之间的大小关系与原数据之间的大小关系一致,即原数据大的对应的新数据也较大。问:若y与x的关系式是 y=x+p(100-x),请说明:当p=
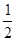 时,这种变换满足上述两个要求。
时,这种变换满足上述两个要求。若按关系式:y=a(x-h)2+k(a﹥0)将数据进行变换,请写出一个满足上述要求的这种关系式。(不要求对关系式符合题意作说明,但要求写出关系式得出的主要过程)

如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P. 设∠BPC=α,如果sinα是方程5x-13x+6=0的根,求cosα的值;
在(1)的条件下,求弦CD的长.
