平面直角坐标系xOy中，抛物线y=ax2-4ax+4a+c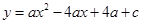
与x轴交于点A、B，与y轴的正半轴交于点C，点A的坐标为（1，0），OB=OC.
（1）求此抛物线的解析式；
（2）若点P是线段BC上的一个动点，过点P作y轴的平行线与抛物线在x轴下方交于点Q，试问线段PQ的长度是否存在最大值？若存在，求出其最大值；若不存在，请说明理由；
（3）若此抛物线的对称轴上的点M满足∠AMC=45°，求点M的坐标.
如图，在△ABC中，AB=AC=10，CB=16，分别以AB、AC为直径作半圆，都经过BC的中点D。则图中阴影部分面积是
甲、乙两名同学进行射击训练，在相同条件下各射靶5次，成绩统计如下：
| 命中环数 |
7 |
8 |
9 |
10 |
| 甲命中相应环数的次数 |
2 |
2 |
0 |
1 |
| 乙命中相应环数的次数 |
1 |
3 |
1 |
0 |
若从甲、乙两人射击成绩方差的角度评价两人的射击水平，则谁的射击成绩更稳定些？
已知一个几何体的三视图和有关的尺寸如图所示，描述该几何体的形状，并根据图中数据计算它的表面积。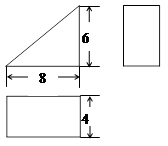
如图，只剪两刀把一个直角三角形分割成三个直角三角形（至少给出三种剪法，用铅笔作出分割线，只要有一条分割线不同，就视作不同的剪法）。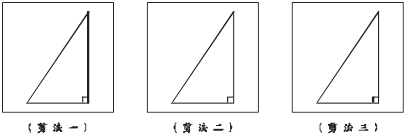
如图甲，已知A、E、F、
C在一条直线上，AE=CF，过E、F分别作DE⊥AC，BF⊥AC。且已知AB=CD。试问DB平分EF能成立吗？请说明理由。
若△DEC的边EC沿AC方向移动，其余条件不变，如图乙，上述结论是否仍成立？请说明理由。
