如图所示,污水处理公司为某楼房建一座周长为30米的三级污水处理池,平面图为矩形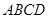 ,
, 米,中间两条隔墙分别为
米,中间两条隔墙分别为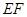 、
、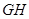 ,池墙的厚度不考虑.
,池墙的厚度不考虑.
(1)用含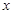 的代数式表示外围墙
的代数式表示外围墙 的长度;
的长度;
(2)如果设计时要求矩形水池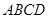 恰好被隔墙分成三个全等的矩形,且它们均与矩形
恰好被隔墙分成三个全等的矩形,且它们均与矩形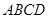 相似,求此时
相似,求此时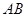 的长;
的长;
(3)如果设计时要求矩形水池 恰好被隔墙分成三个全等的正方形.已知池的外围墙建造单价为每米400元,中间两条隔墙建造单价每米300元,池底建造的单价为每平方米100元.试计算此项工程的总造价.(结果精确到1元)
恰好被隔墙分成三个全等的正方形.已知池的外围墙建造单价为每米400元,中间两条隔墙建造单价每米300元,池底建造的单价为每平方米100元.试计算此项工程的总造价.(结果精确到1元)
(5分)先阅读理解下面的例题,再按要求解答下列问题:
例题:解一元二次不等式x2﹣4>0
解:∵x2﹣4=(x+2)(x﹣2)
∴x2﹣4>0可化为
(x+2)(x﹣2)>0
由有理数的乘法法则“两数相乘,同号得正”,得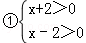
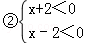
解不等式组①,得x>2,
解不等式组②,得x<﹣2,
∴(x+2)(x﹣2)>0的解集为x>2或x<﹣2,
即一元二次不等式x2﹣4>0的解集为x>2或x<﹣2.
(1)一元二次不等式x2﹣16>0的解集为x>4或x<﹣4;
(2)分式不等式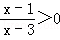 的解集为x>3或x<1 ;
的解集为x>3或x<1 ;
(3)解一元二次不等式2x2﹣3x<0.
我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.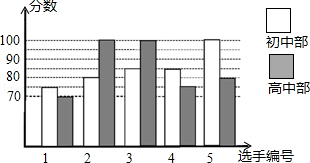
(1)根据图示填写下表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
| 平均数 |
中位数 |
众数 |
|
| 初中部 |
|
85 |
|
| 高中部 |
85 |
|
100 |
如图,△ABC与△ADE关于直线MN对称.BC与DE的交点F在直线MN上.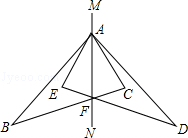
①指出两个三角形中的对称点;
②指出图中相等的线段和角;
③图中还有对称的三角形吗?
如图所示,
(1)在图a中把正方形分成四个全等的三角形;
(2)在图b中把正五边形分成五个全等的三角形;
(3)在图c中把正六边形分成六个全等的三角形?
(4)通过(1)(2)(3)的解答,你发现了什么规律?
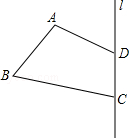
如图,已知四边形ABCD和直线l,试在图形中作四边形A′B′C′D′,使四边形A′B′C′D′和四边形ABCD关于直线l对称.(不要求写作法,只仅留作图痕迹)