(5分)先阅读理解下面的例题，再按要求解答下列问题：
例题：解一元二次不等式x2﹣4＞0
解：∵x2﹣4=（x+2）（x﹣2）
∴x2﹣4＞0可化为
（x+2）（x﹣2）＞0
由有理数的乘法法则“两数相乘，同号得正”，得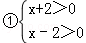
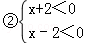
解不等式组①，得x＞2，
解不等式组②，得x＜﹣2，
∴（x+2）（x﹣2）＞0的解集为x＞2或x＜﹣2，
即一元二次不等式x2﹣4＞0的解集为x＞2或x＜﹣2．
（1）一元二次不等式x2﹣16＞0的解集为x＞4或x＜﹣4；
（2）分式不等式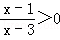
的解集为x＞3或x＜1 ；
（3）解一元二次不等式2x2﹣3x＜0．
如图，在高楼AB前D点测得楼顶A的仰角为30°，向高楼前进60米到达C点处，又测得仰角为45°，求高楼的高度为多少?（结果精确到0.1米，
≈1.414,
≈1.732）
如右图，直线d过正方形ABCD的顶点B，点A，C到直线d的距离分别是
和2，求正方形ABCD的对角线AC的长.
已知点A（k+1，2）在双曲线y= 上，试判断双曲线y= 与直线y=x+1有无交点.
解方程：（a－2）（a－3）="12" .
阅读探究有关个位数是5的整数的平方简便计算问题.
观察下列算式：
152=1×2×100＋25=225；252=2×3×100＋25=625；352=3×4×100＋25=1225……（1）请你写出952的简便计算过程及结果；
（2）其实这种方法也可以推广到个位数是5的三位数的平方，证明略.
① 请你写出1152的简便计算过程及结果.
② 用计算或说理的方式确定9852－8952的结果末两位数字是多少？（3）已知一个个位数是5的整数的平方是354025，请用方程的相关知识求这个数.