已知两点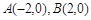
，直线AM、BM相交于点M，且这两条直线的斜率之积为
.
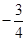（Ⅰ）求点M的轨迹方程；
（Ⅱ）记点M的轨迹为曲线C，曲线C上在第一象限的点P的横坐标为1，直线PE、PF与圆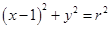
（
）相切于点E、F，又PE、PF与曲线C的另一交点分别为Q、R.
求△OQR的面积的最大值（其中点O为坐标原点）.
已知a>b>0，比较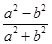
与
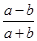的大小．
如图，圆O的直径AB＝8，圆周上过点C的切线与BA的延长线交于点E，过点B作AC的平行线交EC的延长线于点P．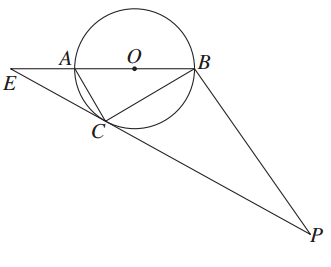
(1)求证：BC2＝AC·BP；
(2)若EC＝2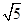
，求PB的长．
如图，△ABO三边上的点C、D、E都在⊙O上，已知AB∥DE，AC＝CB．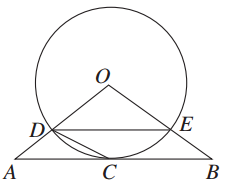
(1)求证：直线AB是⊙O的切线；
(2)若AD＝2，且tan∠ACD＝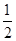
，求⊙O的半径r的长．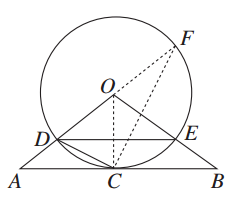
如图所示，已知D为△ABC的BC边上一点，⊙O1经过点B、D交AB于另一点E，⊙O2经过点C、D交AC于另一点F，⊙O1与⊙O2交于点G．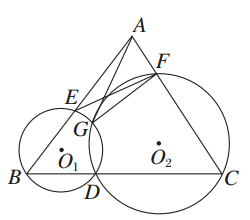
(1)求证：∠EAG＝∠EFG；
(2)若⊙O2的半径为5，圆心O2到直线AC的距离为3，AC＝10，AG切⊙O2于G，求线段AG的长．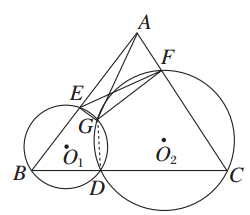
如图所示，⊙O内切△ABC的边于D、E、F，AB＝AC，连接AD交⊙O于点H，直线HF交BC的延长线于点G．求证：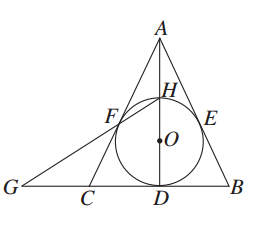
(1)圆心O在直线AD上；
(2)点C是线段GD的中点．