在一分钟投篮测试中,甲、乙两组同学的一次测试成绩如下:
| 成绩 |
4 |
5 |
6 |
7 |
8 |
9 |
| 甲组(人) |
1 |
2 |
4 |
2 |
1 |
5 |
| 乙组(人) |
1 |
1 |
3 |
5 |
2 |
3 |
(1)求甲、乙两组一分钟投篮测试成绩的平均数和方差;
(2)从统计学的角度看,你认为哪组同学的测试成绩较好?为什么?
一个不透明袋子中有 1个红球, 1个绿球和n个白球,这些球除颜色外无其
他差别.
(1)当n=l时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?
(2)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该实验,发现摸到绿球的频率稳定于0.25,则n的值是_
(3)在一个摸球游戏中,所有可能出现的结果如下:
根据树状图呈现的结果,求两次摸出的球额色不同的概率
某公司欲招聘一名工作人员,对甲、乙两位应聘者进行面试和笔试,他们的成绩(百分制)如下表所示.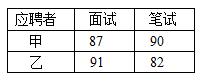
若公司分别赋予面试成绩和笔试成绩6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
如图,抛物线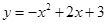 与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.
与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,请解决下列问题.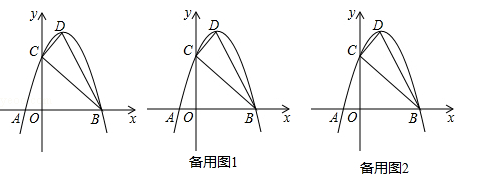
(1)填空:点C的坐标为( , ),点D的坐标为( , );
(2)设点P的坐标为(a,0),当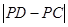 最大时,求a的值并在图中标出点P的位置;
最大时,求a的值并在图中标出点P的位置;
(3)在(2)的条件下,将△BCP沿x轴的正方向平移得到△B′C′P′,设点C对应点C′的横坐标为t(其中0<t<6),在运动过程中△B′C′P′与△BCD重叠部分的面积为S,求S与t之间的关系式,并直接写出当t为何值时S最大,最大值为多少?
国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表: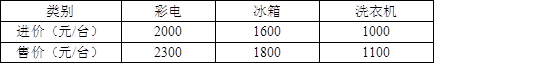
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?