一个不透明袋子中有 1个红球, 1个绿球和n个白球,这些球除颜色外无其
他差别.
(1)当n=l时,从袋中随机摸出1个球,摸到红球和摸到白球的可能性是否相同?
(2)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该实验,发现摸到绿球的频率稳定于0.25,则n的值是_
(3)在一个摸球游戏中,所有可能出现的结果如下:
根据树状图呈现的结果,求两次摸出的球额色不同的概率
(1)计算: ;
(2)先化简,再求值: ,其中 从 ,2,3中取一个你认为合适的数代入求值.
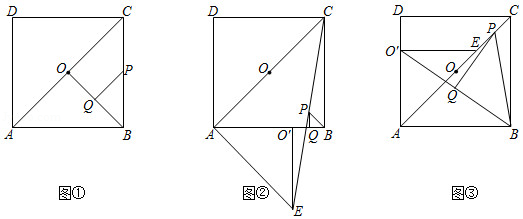
如图,四边形 是正方形,点 为对角线 的中点.
(1)问题解决:如图①,连接 ,分别取 , 的中点 , ,连接 ,则 与 的数量关系是 ,位置关系是 ;
(2)问题探究:如图②,△ 是将图①中的 绕点 按顺时针方向旋转 得到的三角形,连接 ,点 , 分别为 , 的中点,连接 , .判断 的形状,并证明你的结论;
(3)拓展延伸:如图③,△ 是将图①中的 绕点 按逆时针方向旋转 得到的三角形,连接 ,点 , 分别为 , 的中点,连接 , .若正方形 的边长为1,求 的面积.
2020年体育中考,增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数 (人 与时间 (分钟)的变化情况,数据如下表:(表中 表示
|
时间 (分钟) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
人数 (人 |
0 |
170 |
320 |
450 |
560 |
650 |
720 |
770 |
800 |
810 |
810 |
(1)根据这15分钟内考生进入考点的累计人数与时间的变化规律,利用初中所学函数知识求出 与 之间的函数关系式;
(2)如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
(3)在(2)的条件下,如果要在12分钟内让全部考生完成体温检测,从一开始就应该至少增加几个检测点?
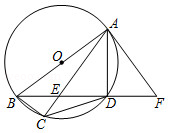
如图, 为 的直径,四边形 内接于 ,对角线 , 交于点 , 的切线 交 的延长线于点 ,切点为 ,且 .
(1)求证: ;
(2)若 , ,求 的值.
第33个国际禁毒日到来之际,贵阳市策划了以“健康人生 绿色无毒”为主题的禁毒宣传月活动,某班开展了此项活动的知识竞赛.学习委员为班级购买奖品后与生活委员对话如下:

(1)请用方程的知识帮助学习委员计算一下,为什么说学习委员搞错了;
(2)学习委员连忙拿出发票,发现的确错了,因为他还买了一本笔记本,但笔记本的单价已模糊不清,只能辨认出单价是小于10元的整数,那么笔记本的单价可能是多少元?