接种疫苗是阻断新冠病毒传播的有效途径，针对疫苗急需问题，某制药厂紧急批量生产，计划每天生产疫苗16万剂，但受某些因素影响，有10名工人不能按时到厂．为了应对疫情，回厂的工人加班生产，由原来每天工作8小时增加到10小时，每人每小时完成的工作量不变，这样每天只能生产疫苗15万剂．
（1）求该厂当前参加生产的工人有多少人？
（2）生产4天后，未到的工人同时到岗加入生产，每天生产时间仍为10小时．若上级分配给该厂共760万剂的生产任务，问该厂共需要多少天才能完成任务？
如图，四边形ABCD是矩形，AB＝6，BC＝8，点E在线段AD上，把△ABE沿直线BE翻折，点A落在点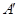
，
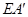的延长线交BC于点F，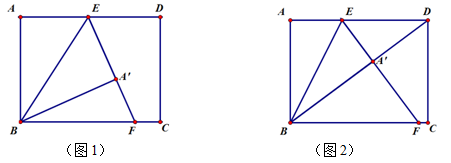
（1）如图（1）求证FE＝FB；
（2）当点E在边AD上移动时，点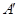的位置也随之变化，
①当点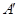恰好落在线段BD上时，如图（2），求AE的长；
②在运动变化过程中，设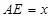
，
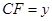，求
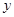与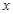
的函数关系式，试判断
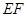能否平分矩形ABCD的面积，若能，求出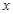的值，若不能，则说明理由；
（3）当点E在边AD上运动时，点D与点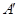之间的距离也随之变化，请直接写出点D与点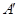之间距离的变化范围．
在平面直角坐标系中，一次函数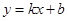
的图象与x轴、y轴相交于点A（
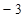，0），B（0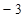，）两点，二次函数
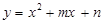的图象经过点A．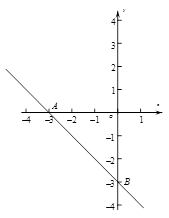
（1）求一次函数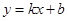的表达式；
（2）若二次函数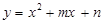的图象的顶点在直线AB上，求m，n；
（3）①设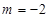
时，当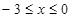
时，求二次函数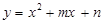的最小值；
②反之若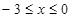时，二次函数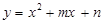的最小值为
，求m，n的值．
如图,在□ABCD中,过A、C、D三点的⊙O交AB于点E,连接DE、CE，∠CDE＝∠BCE．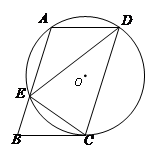
（1）求证：AD＝CE；
（2）判断直线BC与⊙O的位置关系，并说明理由；
（3）若BC＝3，DE＝6，求BE的长．
甲、乙两车分别从A、B两地同时出发相向而行，并以各自的速度匀速行驶，甲车与乙车相遇后休息半小时，再按原速度继续前进到达B地；乙车从B地直接到达A地；两车到达各自目的地后即停止．如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象．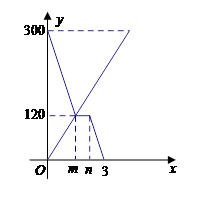
（1）甲车的速度是，m=；
（2）请分别写出两车在相遇前到B地的距离y（千米）与甲车出发时间x（小时）的函数关系式；
（3）当乙车行驶多少时间时，甲乙两车的距离是280千米．
如图，在一笔直的海岸线l上有AB两个观测站，A在B的正东方向，AB=2（单位：km）．有一艘小船在点P处，从A测得小船在北偏西60°的方向，从B 测得小船在北偏东45°的方向．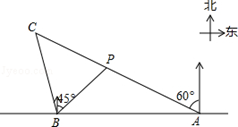
（1）求点P到海岸线l的距离；
（2）小船从点P处沿射线AP的方向航行一段时间后，到点C处，此时，从B测得小船在北偏西15°的方向．求点C与点B之间的距离．（上述两小题的结果都保留根号）