在平面直角坐标系中，一次函数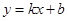
的图象与x轴、y轴相交于点A（
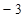，0），B（0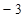，）两点，二次函数
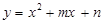的图象经过点A．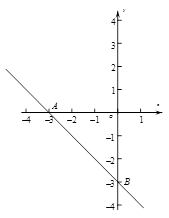
（1）求一次函数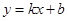的表达式；
（2）若二次函数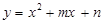的图象的顶点在直线AB上，求m，n；
（3）①设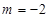
时，当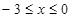
时，求二次函数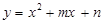的最小值；
②反之若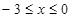时，二次函数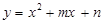的最小值为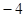
，求m，n的值．
甲、乙两人在5次打靶测试中命中的环数如下：
甲：8，8，7，8，9
乙：5，9，7，10，9
（1）填写下表：
| 平均数 |
众数 |
中位数 |
方差 |
|
| 甲 |
8 |
8 |
0.4 |
|
| 乙 |
9 |
3.2 |
（2）教练根据这5次成绩，选择甲参加射击比赛，教练的理由是什么？
（3）如果乙再射击1次，命中8环，那么乙的射击成绩的方差．（填“变大”、“变小”或“不变”）．
已知：如图，在平行四边形ABCD中，点E、F在AC上，且AE=CF．
求证：四边形BEDF是平行四边形．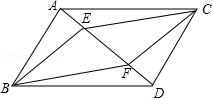
（1）解方程：x2+4x﹣1=0；
（2）解不等式组：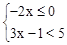
．
（1）计算：
；
（2）计算：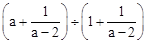
．
在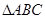
中，AC=25，AB=35，
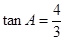，点D为边AC上一点，且AD=5，点E、F分别为边AB上的动点（点F在点E的左边），且∠EDF=∠A.设AE=x，AF=y.
（1）如图1，当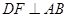
时，求AE的长；
（2）如图2，当点E、F在边AB上时，求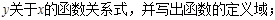
（3）联结CE，当
求
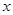的值.