某公园元旦期间,前往参观的人非常多.这期间某一天某一时段,随机调查了部分入园游客,统计了他们进园前等候检票的时间,并绘制成如下图表.表中“10~20”表示等候检票的时间大于或等于10min而小于20min,其它类同.
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)表中a=____,b=_____,并请补全频数分布直方图;
(3)在调查人数里,若将时间分段内的人数绘成扇形统计图,则“40~50”的圆心角的度数是 .
在2008年春运期间,我国南方出现大范围冰雪灾害,导致某地电路断电,该地供电局组织电工进行抢修。供电局距离抢修工地15千米,抢修车装载着所需材料先从供电局出发,15分钟后,电工乘吉普车从同一地点出发,结果他们同时到达抢修工地。已知吉普车速度是抢修车速度的1.5倍,求这两种车的速度.
已知:如图,在直角梯形 中,
中,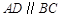 ,
, ,
, ,
, .
.求直角梯形
 的面积;
的面积;点E是
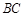 边上一点,过点
边上一点,过点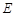 作EF⊥DC于点F.求证
作EF⊥DC于点F.求证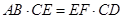 .
.
已知:如图,AB⊥BE于点B,DE⊥BE于点E,F、C在BE上,AC、DF相交于点G,且AB=DE,BF=CE.
求证: GF=GC.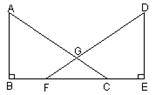
如图,已知抛物线y=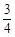 x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为
x2+bx+c与坐标轴交于A、B、C三点, A点的坐标为
(-1,0),过点C的直线y=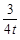 x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
x-3与x轴交于点Q,点P是线段BC上的一个动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.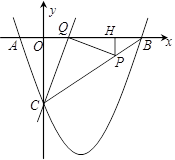
(1)填空:点C的坐标是_ _,b=__;
(2)求线段QH的长(用含t的式子表示);
(3)依点P的变化,是否存在t的值,使以P、H、Q为顶点的三角形与△COQ相似?若存在,求出所有t的值;若不存在,说明理由.
如图1,在□ABCD中,AE⊥BC于E,E恰为BC的中点,AD=AE. (1)如图2,点P在线段BE上,作EF⊥DP于点F,连结AF.
求证: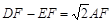 ;
;(2)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF⊥DP于点F,连结AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.