已知:点 B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.
求证:⑴ △ABC≌△DEF;
⑵ BE=CF.
(1)求 值:
值: 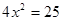 (2)求
(2)求 值:
值: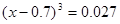

求下列式子的值:
(— 4)2 +2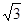 —
— 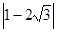 —
—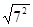 —
—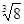
某市政府计划修建一处公共服务设施,使它到三所公寓A、B、C 的距离相等。
(1)若三所公寓A、B、C的位置如图所示,请你在图中确定这处公共服务设施(用点P表示)的位置(尺规作图,保留作图痕迹,不写作法);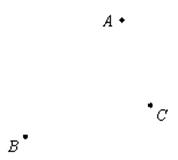
(2)若∠BAC=56º,则∠BPC= º.
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:( 用直尺画图)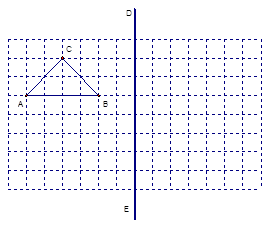
(1)画出格点△AB C(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使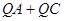 最小。
最小。