阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔 . , 年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉 , 年)才发现指数与对数之间的联系.
对数的定义:一般地,若 ,那么 叫做以 为底 的对数,记作: .比如指数式 可以转化为 ,对数式 可以转化为 .
我们根据对数的定义可得到对数的一个性质: , , , ;理由如下:
设 , ,则 ,
,由对数的定义得
又
解决以下问题:
(1)将指数 转化为对数式 ;
(2)证明 , , ,
(3)拓展运用:计算 .
解方程: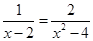 .
.
如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和( ,
, )两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).
)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).
(1)求a,b,c的值;
(2)求证:在点P运动的过程中,⊙P始终与x轴相交;
(3)设⊙P与x轴相交于M(x1,0),N(x2,0)(x1<x2)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(﹣1,﹣1),(0,0),( ,
, ),…都是“梦之点”,显然,这样的“梦之点”有无数个.
),…都是“梦之点”,显然,这样的“梦之点”有无数个.
(1)若点P(2,m)是反比例函数y= (n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(2)函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;
(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),且满足﹣2<x1<2,|x1﹣x2|=2,令t=b2﹣2b+ ,试求出t的取值范围.
,试求出t的取值范围.
如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作⊙O的切线交AC于点E.
(1)求证:DE⊥AC;
(2)若AB=3DE,求tan∠ACB的值.
为建设“秀美幸福之市”,长沙市绿化提质改造工程正如火如荼地进行,某施工队计划购买甲、乙两种树苗共400棵对芙蓉路的某标段道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.
(1)若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?
(2)若购买甲种树苗的金额不少于购买一中树苗的金额,至少应购买甲种树苗多少棵?