城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客需求,为此,某市公交公司在某站台的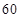 名候车乘客中随机抽取
名候车乘客中随机抽取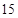 人,将他们的候车时间作为样本分成
人,将他们的候车时间作为样本分成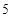 组,如下表所示(单位:min):
组,如下表所示(单位:min):
| 组别 |
候车时间 |
人数 |
| 一 |
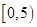 |
 |
| 二 |
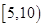 |
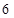 |
| 三 |
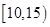 |
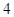 |
| 四 |
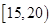 |
 |
| 五 |
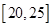 |
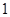 |
(1)求这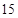 名乘客的平均候车时间;
名乘客的平均候车时间;
(2)估计这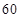 名乘客中候车时间少于
名乘客中候车时间少于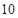 分钟的人数;
分钟的人数;
(3)若从上表第三、四组的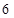 人中选
人中选 人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
设关于 的一元二次方程
的一元二次方程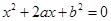
(Ⅰ)若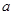 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,
是从0,1,2三个数中任取的一个数,
求上述方程有实数根的概率;
(Ⅱ)若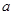 是从区间
是从区间 任取的一个数,
任取的一个数, 是从区间
是从区间 任取的一个数,求上述方程有实数根的概率.
任取的一个数,求上述方程有实数根的概率.
为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为 分)作为样本(样本容量为
分)作为样本(样本容量为 )进行统计.按照
)进行统计.按照 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在 的数据).
的数据).
(1)求样本容量 和频率分布直方图中的
和频率分布直方图中的 、
、 的值;
的值;
(2)在选取的样本中,从竞赛成绩在 分以上(含
分以上(含 分)的学生中随机抽取
分)的学生中随机抽取 名学生参加“中国谜语大会”,求所抽取的
名学生参加“中国谜语大会”,求所抽取的 名学生中至少有一人得分在
名学生中至少有一人得分在 内的概率.
内的概率.
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村 到
到 年五年间每年考入大学的人数,为了方便计算,
年五年间每年考入大学的人数,为了方便计算, 年编号为
年编号为 ,
,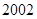 年编号为
年编号为 ,……,
,……, 年编号为
年编号为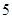 ,数据如下:
,数据如下:
根据这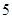 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出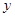 关于
关于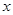 的回归方程
的回归方程 ,并计算第
,并计算第 年的估计值.
年的估计值.
参考:用最小二乘法求线性回归方程系数公式
已知两个关于x的一元二次方程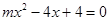 和
和 ,求两方程的根都是整数的充要条件.
,求两方程的根都是整数的充要条件.
已知 ,
,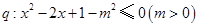 ,若
,若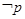 是
是 的必要而不充分条件,求实数
的必要而不充分条件,求实数 的取值范围.
的取值范围.