如图,热气球的探测器显示,从热气球点A处看我市一栋高楼顶部B点处的仰角为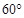 ,看这栋高楼底部C点处的仰角为
,看这栋高楼底部C点处的仰角为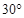 ,热气球与高楼的水平距离为66m,求这栋高楼的高度.(结果精确到
,热气球与高楼的水平距离为66m,求这栋高楼的高度.(结果精确到 ,参考数据:
,参考数据: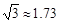 )
)
学校图书馆上周借书记录如下(超过50册的部分记为正,少于50册的部分记为负):
(1)上星期五借出图书________册.
(2)上星期二比上星期五多借出图书________册。
(3)上周平均每天借出图书多少册?(一周以5天计算)
把下列各数化简后在数轴上表示出来,并把它们按从小到大的顺序用“<”号连接起来。



(1)
(2)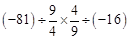
(3)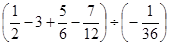
(4)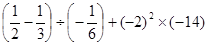
(5) 
(6)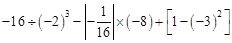
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.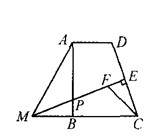
(1)若∠MFC=120°,求证:AM=2MB;
(2)求证:∠MPB=90°-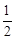 ∠FCM.
∠FCM.
若△ABC的三边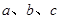 满足条件:a2+b2+c2+338=10a+24b+26c,试判断△ABC的形状.
满足条件:a2+b2+c2+338=10a+24b+26c,试判断△ABC的形状.