如图是二次函数y=x2﹣2x﹣3的图象.
(1)求该抛物线的顶点坐标、与x轴的交点坐标
(2)观察图象直接指出x在什么范围内时,y>0?
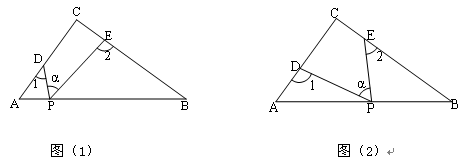
RtΔABC中,∠C=90°,点D、E分别是ΔABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠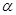 .
.
(1)若点P在线段AB上,如图(1)所示,且∠ =50°,则∠1+∠2=°;
=50°,则∠1+∠2=°;
(2)若点P在边AB上运动,如图(2)所示, 则∠ 、∠1、∠2之间的关系为:
、∠1、∠2之间的关系为:
;
(3)若点P运动到边AB的延长线上,如图(3)所示,则∠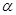 、∠1、∠2之间有何关系?猜想并说明理由。
、∠1、∠2之间有何关系?猜想并说明理由。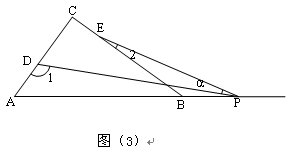
(4)若点P运动到ΔABC形外,如图(4)所示,则∠ 、∠1、∠2之间的关系为:
、∠1、∠2之间的关系为:
;
如图所示,现有边长分别为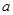 、
、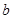 的正方形、邻边长为
的正方形、邻边长为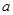 和
和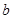 (
(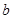 >
>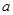 )的长方形硬纸板若干.
)的长方形硬纸板若干.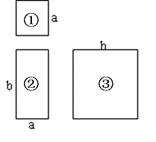
(1)从这三种硬纸板中选择一些拼出面积为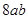 的不同形状的长方形,则这些长方形的周长共有___________种不同情况;
的不同形状的长方形,则这些长方形的周长共有___________种不同情况;
(2)请选择适当形状和数量的硬纸板,拼出面积为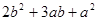 的长方形,画出拼法的示意图;
的长方形,画出拼法的示意图;
(3) 取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为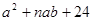 ,则n可能的整数值有_____个;
,则n可能的整数值有_____个;
(4)已知长方形②的周长为10,面积为3,求小正方形①与大正方形③的面积之和。
同学们,你们会用画多边形的对角线来解决生活中的数学问题吗?
比如,学校举办足球赛,共有5个班级的足球队参加比赛,每个队都要和其他各队比赛一场,根据积分排列名次.问学校一共要安排多少场比赛?
我们画出5个点,每个点各代表一个足球队,两个队之间比赛一场就用一条线段把它们连接起来.由于每个队都要与其他各队比赛一场,这样每个点与另外4个点都会有一条线段连接(如图).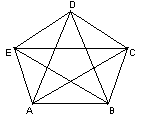
现在我们只要数一数五边形的边数和它的对角线条数就可以了.由图可知,五边形的边数和对角线条数都是5,所以学校一共要安排10场比赛.
同学们,请用类似的方法来解决下面的问题:
真真、明明、可可、飞飞、红红和娜娜六人参加一次会议,见面时他们相互握手问好.已知真真已握了5次手,明明已握了4次手,可可已握了3次手,飞飞已握了2次手,红红握手1次,请推算出娜娜目前已和哪几个人握了手.
如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36
…………………………
(1)表中第10行的最后一个数是______________,它是自然数_____________的平方,第10行共有____________个数;
(2)用含n的代数式表示:第n行的第一个数是___________________,最后一个数是________________,第n行共有_______________个数;
(3)求第n行各数之和.
如图,在 按要求完成下列各题.
按要求完成下列各题.
(1)作△ABC的高AD;
(2)作△ABC的角平分线AE;
(3)若
根据你所画的图形算出∠DAE的度数为 ;
(4)探究:小明认为如果只知道∠C-∠B= 40°,
也能得出∠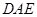 的度数?你认为可以吗?
的度数?你认为可以吗?
若能,请你写出求解过程;若不能,请说明理由.