如图,已知反比例函数 (m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(m是常数,m≠0),一次函数y=ax+b(a、b为常数,a≠0),其中一次函数与x轴,y轴的交点分别是A(-4,0),B(0,2).
(1)求一次函数的关系式;
(2)反比例函数图象上有一点P满足:①PA⊥x轴;②PO= (O为坐标原点),求反比例函数的关系式;
(O为坐标原点),求反比例函数的关系式;
(3)求点P关于原点的对称点Q的坐标,判断点Q是否在该反比例函数的图象上.
⑴ |-4|+(-3)2-23-(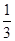 )-1
)-1
⑵ 2m·m2+(2m3)2÷m3
⑶ -3(x2-xy)+x(-2y+2x)
⑷ (2a-3b)2-(b+3a)(3a-b)
生活中,有人喜欢把传送的便条折成 形状,折叠过程是这样的(阴影部分表示纸条的反面):
形状,折叠过程是这样的(阴影部分表示纸条的反面):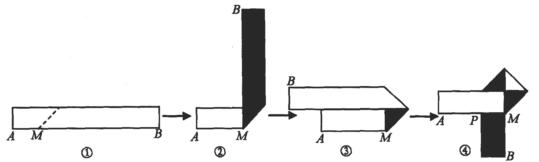
如果由信纸折成的长方形纸条(图①)长为26厘米,回答下列问题:
(1)如果长方形纸条的宽为2厘米,并且开始折叠时起点M与点A的距离为3厘米,那么在图②中,BM=_____厘米;在图④中,BM=_____厘米.
(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是对称图形,假设长方形纸条的宽为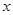 厘米,试求在开始折叠时(图①)起点M与点A的距离(用含
厘米,试求在开始折叠时(图①)起点M与点A的距离(用含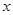 的代数式表示).
的代数式表示).
如图,已知AD∥CB,AP平分∠DAB,CP平分∠BCD,∠D=40°,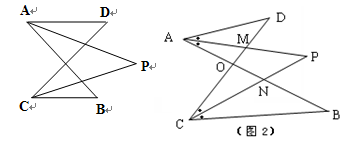
试求:(1)∠PCB的度数;
(2)若∠B=36°,试求∠P的度数.
(3)在图2中,若AD与CB不平行,∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求∠P的度数.
画图并填空: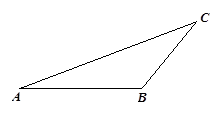
① 画出图中△ABC的高AD(标注出点D的位置);
② 画出将△ABC沿射线AB方向平移2cm后得到的△A1B1C1;
③ 根据“图形平移”的性质,得:BB1=cm;线段AC与线段A1C1的关系是.
解方程组:(本题共8分,每题4分).
(1)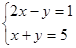
(2)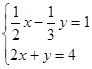 ①②
①②