如图,在多面体ABCDEF中,底面ABCD是边长为2的正方形,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.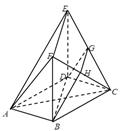
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求证:平面BDGH//平面AEF;
(Ⅲ)求多面体ABCDEF的体积.
(本小题12分)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度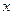 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当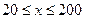 时,车流速度v是车流密度
时,车流速度v是车流密度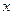 的一次函数.
的一次函数.
(Ⅰ)当 时,求函数
时,求函数 的表达式;
的表达式;
(Ⅱ)当车流密度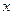 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时)
可以达到最大,并求出最大值(精确到1辆/小时)
(本小题12分)已知 ,求下列各式的值:
,求下列各式的值:
(1) ;(2)
;(2) .
.
(本小题12分)已知集合 ,集合
,集合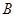 是函数
是函数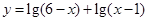 的定义域,
的定义域,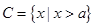 ,
,  .
.
(1)求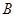 ; (2)求
; (2)求 ;(3)如果
;(3)如果 ,求
,求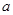 的取值范围
的取值范围
(本小题12分)计算下列各式的值:
(1)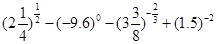 ;(2)
;(2)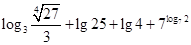
已知幂函数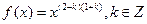 ,且
,且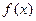 在
在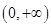 上单调递增.
上单调递增.
(Ⅰ)求实数 的值,并写出相应的函数
的值,并写出相应的函数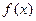 的解析式;
的解析式;
(II)若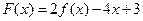 在区间
在区间 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(III)试判断是否存在正数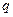 ,使函数
,使函数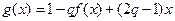 在区间
在区间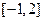 上的值域为
上的值域为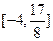 . 若存在,求出
. 若存在,求出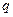 的值;若不存在,请说明理由
的值;若不存在,请说明理由