在地面上方某处的真空室里存在着水平向左的匀强电场,以水平向右和竖直向上为x轴、y轴正方向建立如图所示的平面直角坐标系。一质量为m、电荷量为+q的微粒从点P(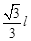 ,0)由静止释放后沿直线PQ运动。当微粒到达点Q(0,-l)的瞬间,撤去电场同时加上一个垂直于纸面向外的匀强磁场(图中未画出),磁感应强度的大小
,0)由静止释放后沿直线PQ运动。当微粒到达点Q(0,-l)的瞬间,撤去电场同时加上一个垂直于纸面向外的匀强磁场(图中未画出),磁感应强度的大小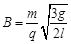 ,该磁场有理想的下边界,其他方向范围无限大。已知重力加速度为g。求:
,该磁场有理想的下边界,其他方向范围无限大。已知重力加速度为g。求: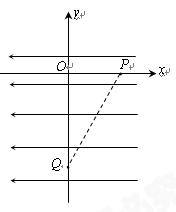
(1)匀强电场的场强E的大小;
(2)撤去电场加上磁场的瞬间,微粒所受合外力的大小和方向;
(3)欲使微粒不从磁场下边界穿出,该磁场下边界的y轴坐标值应满足什么条件?
继1999年11月20日我国“神州一号”无人驾驶载人飞船的成功发射和回收后,我国又已经成功发送了“神州二号”、“神州三号”、“神州四号”无人宇宙飞船。所了解,我国将要按计划发送首架载人航天飞船——“神州五号”上天。届时我国宇宙员将乘我国自行研制的载人飞船遨游太空。
(1)为了使飞船到达上述速度需要一个加速过程,在加速过程中,宇航员处于超重状态。人们把这种状态下宇航员对座椅的压力与静止在地球表面时的重力的比值称为耐受力值,用k表示。选择宇航员时,要求他在此状态下的耐受力值为4 ≤ k ≤ 12,试求飞船在竖直向上发射时的加速度值的变化范围;
(2)若飞船绕地球运行的轨道离地面高度为400km,已知地球半径为6400km,地球表面重力加速度g=10m/s2,求此飞船的速度。(保留2位有效数字)
如图14所示,车厢内的小桌上固定一光滑斜面,除去小球车厢的总质量为M、小球的质量为m,斜面倾角为α。车在水平推力作用下向右做匀加速直线运动,小球(视为质点)始终与车相对静止,小球距桌面的高度为h,距车厢地板高度为H,离桌面边缘水平距离为L,离车厢前壁的距离为d。车在运动过程中所受的阻力等于车对地面压力的k倍,重力加速度为g。
(1)求水平推力F1的大小
(2)若M=10kg,m=1kg,α=37°, k=0.20,h=0.20m,H=0.80m,L=0.30m,d=1.60m,g=10m/s2。当车速为v0=15m/s时,撤去推力F1同时对车施加水平向左的拉力F2(如虚线所示),小球立即离开斜面向右飞去。为使小球在运动中不碰到桌子和前壁,所加拉力F2应满足什么条件?
如图13所示,半径为R、内径很小的光滑半圆轨道竖直放置在水平地面上,两个质量为m的小球A、B(直径略小于管内径),以不同速度进入管内。A通过轨道的最高点C时,对管壁恰好无弹力的作用。A、B两球落地点的水平距离为4R,求:B球在最高点C对管壁的弹力大小和方向。(两球离开管后在同一竖直面内运动)
哈尔滨冰雪大世界集天下冰雪艺术精华,融冰雪娱乐活动于一园,是当今世界规模最大、冰雪艺术景观最多、冰雪娱乐项目最全、夜晚景色最美的冰雪大世界游园会,至今已举办了十一届。在第十一届冰雪大世界景区建有一大型冰滑梯,该冰滑梯可看成倾角θ=30°长为50米的斜面。一名游客总质量m=60kg,他从静止开始匀加速下滑,在时间t=5s内滑至冰滑梯底端。(不计空气阻力,取g=10m/s2,结果保留2位有效数字)问:
(1)游客与滑梯冰面间动摩擦因数μ1为多大?
(2)游客从滑梯滑下后在水平地面上沿直线向前滑行(游客由滑梯底端滑至水平面时速度大小不变、方向变为水平),若游客与水平地面间的动摩擦因数μ2=0.5,求游客在水平地面上滑行多远后停下?
如图所示。两极板A、B间有场强为E=200N/C的匀强电场,一带电荷量 的小球开始时静止在电场中的P点,靠近电场极板B处有一挡板S,小球与挡板S的距离
的小球开始时静止在电场中的P点,靠近电场极板B处有一挡板S,小球与挡板S的距离 ,与A板距离
,与A板距离 ,小球的重力不计。在电场力作用下小球向左运动,与挡板S相碰后电量减少到碰前的k倍,已知
,小球的重力不计。在电场力作用下小球向左运动,与挡板S相碰后电量减少到碰前的k倍,已知 ,碰撞过程中小球的机械能没有损失。(
,碰撞过程中小球的机械能没有损失。(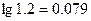 )求:
)求:
(1)小球第一次到达挡板S时的动能;
(2)小球第一次与挡板S相碰后向右运动的距离;
(3)小球与挡板S经过多少次碰撞后,才能运动到A板?