如图14所示,车厢内的小桌上固定一光滑斜面,除去小球车厢的总质量为M、小球的质量为m,斜面倾角为α。车在水平推力作用下向右做匀加速直线运动,小球(视为质点)始终与车相对静止,小球距桌面的高度为h,距车厢地板高度为H,离桌面边缘水平距离为L,离车厢前壁的距离为d。车在运动过程中所受的阻力等于车对地面压力的k倍,重力加速度为g。
(1)求水平推力F1的大小
(2)若M=10kg,m=1kg,α=37°, k=0.20,h=0.20m,H=0.80m,L=0.30m,d=1.60m,g=10m/s2。当车速为v0=15m/s时,撤去推力F1同时对车施加水平向左的拉力F2(如虚线所示),小球立即离开斜面向右飞去。为使小球在运动中不碰到桌子和前壁,所加拉力F2应满足什么条件?
如图所示,倾角θ=37°的斜面底端B平滑连接着半径r=0.40m的竖直光滑圆轨道。质量m=0.50kg的小物块,从距地面h=2.7m处沿斜面由静止开始下滑,小物块与斜面间的动摩擦因数μ=0.25,求:(sin37°=0.6,cos37°=0.8,g=10m/s2)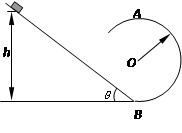
(1)物块滑到斜面底端B时的速度大小。
(2)物块运动到圆轨道的最高点A时,对圆轨道的压力大小。
如图所示,质量M=1kg的木板静止在粗糙的水平地面上,木板与地面间的动摩擦因数μ1=0.1,在木板的左端放置一个质量m=1kg,大小可忽略的铁块,铁块与木板间的动摩擦因数μ2=0.4,g取10m/s2,试求:
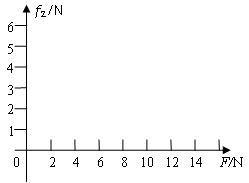
(1)若木板长L=1m,在铁块上加一个水平向右的恒力F=8N,经过多长时间铁块运动到木板的右端?
(2)若在铁块右端施加一个从零开始连续增大的水平向右的力F,假设木板足够长,在图中画出铁块受到木板的摩擦力f2随拉力F大小的变化而变化的图象。
如图甲所示为一皮带传送装置,皮带保持匀速率运动,货物由静止放到皮带顶端,被皮带向下传送,其运动的v—t图象如图乙所示,g=10m/s2。求:(1)皮带的速率;(2)皮带与水平面间的夹角q及货物与皮带之间的动摩擦因数m;(3)如果货物是用麻袋装载的石灰粉,当第一件货物被运送后,发现皮带上留有一段8.0m长的白色痕迹,请由此推断每件货物的传送时间和传送距离。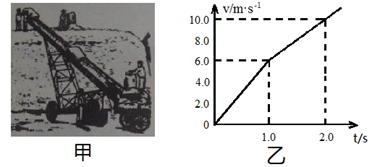
一玩具火车A的制动性能经如下测定:当它以0.2 m/s的速度在水平平直轨道上行驶时,在制动后需要40 s才能停下.现这列玩具火车正以0.2 m/s的速度在水平轨道上行驶,在其前方60 cm处有另一玩具火车B正以0.04m/s的速度在一旁的平行轨道上同向行驶.现对玩具火车A采取制动措施,问:两车是否会发生会车?如果能会发生几次会车?会车发生在什么时刻?
消防车的供水系统主要由水泵、输水管道和水炮组成。如图所示,消防水炮离地高度为H,建筑物上的火点离地高度为h,水炮与火点的水平距离为x,水泵的功率为P,整个供水系统的效率η=0.6。假设水从水炮水平射出,其中水泵、输水管道没有画出,水泵放置于地面,不计空气阻力,取g=10m/s2。
(1)、若H=80m,h=60m,水炮出水速度v0=30m/s,试求水炮与起火建筑物之间的水平距离x;
(2)、在(1)问中,若水炮每秒出水量m0="60" kg,试求水泵的功率P;
(3)、当完成高层灭火后,还需要对散落在火点正下方地面上的燃烧物进行灭火,将水炮竖直下移至H´=45m,假设供水系统的效率η不变,水炮出水口的横截面积不变,水泵功率应调整为P´,则P´应为多大?