如图,等边△ABC的边长为4,E是边BC上的动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE＝EB．设EC＝x（0＜x≤2）．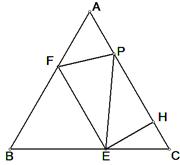
（1）请直接写出图中与线段EF相等的两条线段（不再另外添加辅助线）；
（2）Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求平行四边形EFPQ的面积（用含
的代数式表示）；
（3）当（2）中 的平行四边形EFPQ面积最大值时,以E为圆心,r为半径作圆,根据⊙E与此时平行四边形EFPQ四条边交点的总个数,求相应的r的取值范围．
如图，已知函数y=﹣x+b的图象与x轴、y轴分别交于点A、B，与函数y=x的图象交于点M，点M的横坐标为2，在x轴上有一点P（a，0）（其中a＞2），过点P作x轴的垂线，分别交函数y=﹣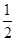
x+b和y=x的图象于点C、D．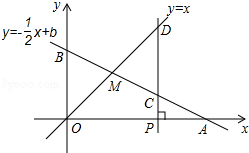
（1）求点A的坐标；
（2）若OB=CD，求a的值．
已知：如图，在△ABC中，AB=AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E．
（1）求证：△ABD≌△CAE；
（2）连接DE，线段DE与AB之间有怎样的位置和数量关系？请证明你的结论．
一家服装店老板到厂家选购A、B两种型号的服装，若购进A种型号服装9件，B种型号服装10件，需要1810元；若购进A种型号服装12件，B种型号服装8件，需要1880元．问A、B两种型号的服装每件分别为多少元？
将某雷达测速区监测到的一组汽车的时速数据整理，得到其频数分布表（未完成）：
| 数据段 |
30～40 |
40～50 |
50～60 |
60～70 |
70～80 |
总计 |
| 频数 |
10 |
40 |
|
|
20 |
|
| 百分比 |
5% |
|
40% |
|
10% |
|
注：30～40为时速大于等于30千米而小于40千米，其他类同．
（1）请你把表中的数据填写完整；
（2）补全频数分布直方图；
（3）如果此路段汽车时速超过60千米即为违章，则违章车辆共有多少辆？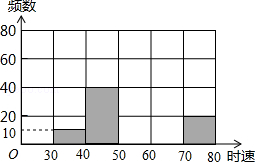
如图，已知：DF∥AC，∠C=∠D．求证：BD∥CE．