商场销售某种冰箱,该种冰箱每台进价为2500元,已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了x元.
(1)填表(不需化简):
| |
每天的销售量/台 |
每台销售利润/元 |
| 降价前 |
8 |
400 |
| 降价后 |
|
|
(2)商场为使这种冰箱平均每天的销售利润达到5000元,则每台冰箱的实际售价应定为多少元?
如图1,点P为四边形ABCD所在平面上的点,如果∠PAD=∠PBC,则称点P为四边形ABCD关于A、B的等角点,以点C为坐标原点,BC所在直线为x轴建立平面直角坐标系,点B的横坐标为﹣6.
(1)如图2,若A、D两点的坐标分别为A(﹣6,4)、D(0,4),点P在DC边上,且点P为四边形ABCD关于A、B的等角点,则点P的坐标为 ;
(2)如图3,若A、D两点的坐标分别为A(﹣2,4)、D(0,4).
①若P在DC边上时,则四边形ABCD关于A、B的等角点P的坐标为 ;
②在①的条件下,将PB沿x轴向右平移m个单位长度(0<m<6)得到线段P′B′,连接P′D, B′D,试用含m的式子表示P′D2+B′D2,并求出使P′D2+B′D2取得最小值时点P′的坐标;
③如图4,若点P为四边形ABCD关于A、B的等角点,且点P坐标为(1,t),求t的值;
④以四边形ABCD的一边为边画四边形,所画的四边形与四边形ABCD有公共部分,若在所画的四边形内存在一点P,使点P分别是各相邻两顶点的等角点,且四对等角都相等,请直接写出所有满足条件的点P的坐标.
在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题: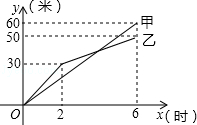
(1)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(2)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?
如图,将▱ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠ABC,连接AC、BE.求证:四边形ABEC是矩形.
如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF.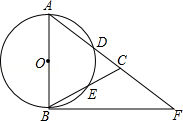
(1)试判断直线BF与⊙O的位置关系,并说明理由;
(2)若AB=6,BF=8,求tan∠CBF.
如图,在一笔直的海岸线l上有A、B两个观测站,点A在点B的正东方向,AB=4km,有一艘小船在点P处,从点A 测得小船在北偏西60°方向,从点B测得小船在北偏东45°的方向.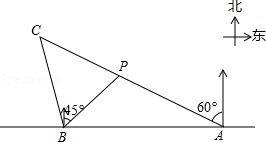
(1)求小船到海岸线l的距离;
(2)小船从点P沿射线AP方向航行一段时间后,到C处,此时,从点B测得小船在北偏西15°的方向,求此时小船到观测点B的距离.(结果保留根号)