如图所示，倾斜轨道AB的倾角为37o，CD、EF轨道水平，AB与CD通过光滑圆弧管道BC连接，CD右端与竖直光滑圆周轨道相连。小球可以从D进入该轨道，沿轨道内侧运动，从E滑出该轨道进入EF水平轨道。小球由静止从A点释放，已知AB长为5R，CD长为R，重力加速度为g，小球与斜轨AB及水平轨道CD、EF的动摩擦因数均为0.5，sin37o=0.6，cos37o=0.8，圆弧管道BC入口B与出口C的高度差为1.8R。求：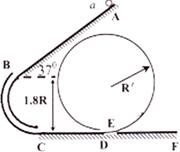
⑴小球滑到斜面底端C时速度的大小。
(2)小球对刚到C时对轨道的作用力。
(3)要使小球在运动过程中不脱离轨道，竖直圆周轨道的半径R’应该满足什么条件？若R’=2.5R，小球最后所停位置距D（或E）多远？
注：在运算中，根号中的数值无需算出。
2010·兰州模拟)荡秋千是大家喜爱的一项体育运动．随着科技迅速发展，将来的某一天，同学们也会在其他星球上享受荡秋千的乐趣．假设你当时所在星球的质量为M，半径为R，可将人视为质点，秋千质量不计、摆长不变、摆角小于90°，引力常量为G.那么：
(1)该星球表面附近时重力加速度g星等于多少？
(2)若经过最低位置的速度为v0，你能上升的最大高度是多少？
如图所示，倾角为θ=30°的足够长的固定斜面上，在底端0处固定一垂直斜面的档板，斜面上OM段光滑，M点及以上均粗糙。质量为m的物块A在M点恰好能静止，有一质量为2m的光滑小物块B以初速度
自N点滑向物块A，已知MN=L，AB间每次碰撞后即紧靠在一起但不粘连，每次AB与档板碰撞后均原速率弹回，求：
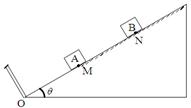
(1)A、B第一次碰撞后紧靠在一起的初速度
；
(2)物块A在M点上方时，离M点的最大距离s；
(3)系统由于摩擦和碰撞所产生的总内能E。
如图，在xoy直角坐标系中，在第三象限有一平行x轴放置的平行板电容器，板间电压U=1×102V。现有一质量m=1.0×10-12kg，带电量q=2.0×10-10C的带正电的粒子(不计重力)，从下极板处由静止开始经电场加速后通过上板上的小孔，垂直x轴从A点进入第二象限的匀强磁场中。磁场方向垂直纸面向外，磁感应强度B=1T。粒子在磁场中转过四分之一圆周后又从B点垂直y轴进入第一象限，第一象限中有平行于y轴负方向的匀强电场E，粒子随后经过x轴上的C点，已知OC=1m。求：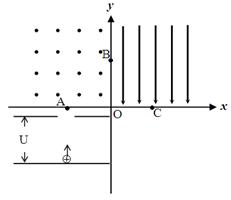
(1)粒子在磁场中做匀速圆周运动的半径r。
(2)第一象限中匀强电场场强E的大小。
【2012• 湖南模拟】如图所示，处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距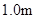
，导轨平面与水平面成θ=37°角，下端连接阻值为
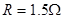的电阻。匀强磁场大小
、方向与导轨平面垂直．质量为
、电阻
的金属棒放在两导轨上，棒与导轨垂直并保持良好接触，它们之间的动摩擦因数为0.25（已知
，
，取g＝10m／s2) 。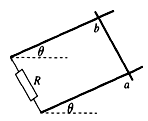
(1)求金属棒沿导轨由静止开始下滑时的加速度大小；
(2)求金属棒稳定下滑时的速度大小及此时ab两端的电压Uab为多少；
(3)当金属棒下滑速度达到稳定时，机械能转化为电能的效率是多少（保留2位有效数字）。
【2012• 北京市西城区期末】如图所示，光滑金属直轨道MN和PQ固定在同一水平面内，MN、PQ平行且足够长，两轨道间的宽度L＝0.50m。轨道左端接一阻值R=0.50Ω的电阻。轨道处于磁感应强度大小B＝0.40T，方向竖直向下的匀强磁场中。质量m=0.50kg的导体棒ab垂直于轨道放置。在沿着轨道方向向右的力F作用下，导体棒由静止开始运动，导体棒与轨道始终接触良好并且相互垂直。不计轨道和导体棒的电阻，不计空气阻力。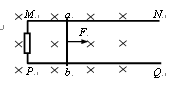
（1）若力F的大小保持不变，且F=1.0N。求
a．导体棒能达到的最大速度大小vm；
b．导体棒的速度v=5.0m/s时，导体棒的加速度大小a。
（2）若力F的大小是变化的，在力F作用下导体棒做初速度为零的匀加速直线运动，加速度大小a=2.0m/s2。从力F作用于导体棒的瞬间开始计时，经过时间t=2.0s，求力F的冲量大小I。