已知半径为2,圆心在直线 上的圆C.
上的圆C.
(Ⅰ)当圆C经过点A(2,2)且与 轴相切时,求圆C的方程;
轴相切时,求圆C的方程;
(Ⅱ)已知E(1,1),F(1,-3),若圆C上存在点Q,使 ,求圆心的横坐标
,求圆心的横坐标 的取值范围.
的取值范围.
在“灿烂阳光小歌手PK赛”10进6的比赛中,有男歌手和女歌手各3人进入前6名,现从中任选2名歌手去参加2010年的元旦联欢会的演出,求:
(1)恰有一名参赛歌手是男歌手的概率;
(2)至少有一名参赛歌手是男歌手的概率;
(3)至多有一名参赛歌手是男歌手的概率.
2008年在中国北京成功举行了第29界奥运赛,其中乒乓球比赛实行五局三胜的规则,即先胜三局的获胜,比赛到此宣布结束。在赛前,有两个国家进行了友谊赛,比赛双方并没有全部投入主力,两队双方较强的队伍每局取胜的概率为0.6,若前四局出现2比2平局,较强队就更换主力,则其在决赛局中获胜的概率为0.7,设比赛结束时的局数为
(1)求 的概率分布;
的概率分布;
(2)求E .
.
造船厂年造船量20艘,造船 艘产值函数为
艘产值函数为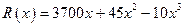 (单位:万元),成本函数
(单位:万元),成本函数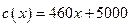 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数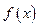 的边际函数
的边际函数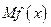 定义为
定义为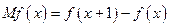
(1)求利润函数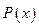 及边际利润函数
及边际利润函数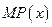 (利润=产值—成本)
(利润=产值—成本)
(2)问年造船量安排多少艘时,公司造船利润最大
(3)边际利润函数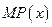
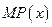 的单调递减区间
的单调递减区间
某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产1百件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为5百件,产品销售数量为t(百件)时,销售所得的收入为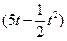 万元
万元
(1)该公司这种产品的年生产量为x百件,生产并销售这种产品所得到的利润为当年产量x的函数f(x),求f(x);
(2)当该公司的年产量为多大时当年所获得的利润最大.
定义在定义域D内的函数y=f(x),若对任意的x1、x2∈D,都有|f(x1)-f(x2)|<1,则称函数y=f(x)为“Storm函数”.已知函数f(x)=x3-x+a(x∈[-1,1],a∈R).
(1)若 ,求过点
,求过点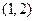 处的切线方程;
处的切线方程;
(2)函数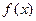 是否为“Storm函数”?如果是,请给出证明;如果不是,请说明理由.
是否为“Storm函数”?如果是,请给出证明;如果不是,请说明理由.