(16分)如图所示,在坐标系的第一、四象限存在一宽度为a、垂直纸面向外的有界匀强磁场,磁感应强度的大小为B;在第三象限存在与y轴正方向成θ=60°角的匀强电场。一个粒子源能释放质量为m、电荷量为+q的粒子,粒子的初速度可以忽略。粒子源在点P(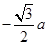 ,
,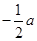 )时发出的粒子恰好垂直磁场边界EF射出;将粒子源沿直线PO移动到Q点时,所发出的粒子恰好不能从EF射出。不计粒子的重力及粒子间相互作用力。求:
)时发出的粒子恰好垂直磁场边界EF射出;将粒子源沿直线PO移动到Q点时,所发出的粒子恰好不能从EF射出。不计粒子的重力及粒子间相互作用力。求:
⑴匀强电场的电场强度;
⑵PQ的长度;
⑶若仅将电场方向沿顺时针方向转动60º角,粒子源仍在PQ间移动并释放粒子,试判断这些粒子第一次从哪个边界射出磁场并确定射出点的纵坐标范围。
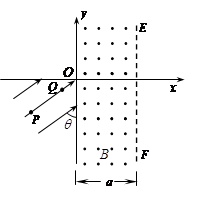
如图所示,直线MN上方存在垂直纸面向里、磁感应强度大小为B的匀强磁场,现有一质量为m、带电荷量为+q的粒子在纸面内以某一速度从A点射入,其方向与MN成30°角,A点到MN的垂直距离为d,带电粒子重力不计.若粒子进入磁场后再次从磁场中射出时恰好能回到A点,求:粒子在磁场中运动的时间t和粒子运动速度的大小v?
如图所示,在第一象限内有垂直纸面向里的匀强磁场,一对正、负离子(质量相同,电荷量相同,重力不计)分别以相同速度沿与x轴成30°角从原点射入磁场,则正、负电子在磁场中运动时间之比为
如图,在第一象限存在匀强磁场,磁感应强度方向垂直于纸面(xy平面)向外;在第四象限存在匀强电场,方向沿x轴负向。在y轴正半轴上某点以与x轴正向平行、大小为v0的速度发射出一带正电荷的粒子,该粒子在(d,0)点沿垂直于x轴的方向进入电场。不计重力。若该粒子离开电场时速度方向与y轴负方向的夹角为θ,求: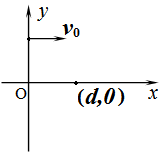
(1)电场强度大小与磁感应强度大小的比值;
(2)该粒子在电场中运动的时间。
如图所示,充电后的平行板电容器水平放置,电容为C,极板间距离为d,上极板正中有一小孔。质量为m、电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板处速度恰为零(空气阻力忽略不计,极板间电场可视为匀强电场,重力加速度为g)。求: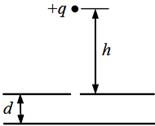
(1)小球到达小孔处的速度;
(2)极板间电场强度大小和电容器所带电荷量;
如图所示,两平行金属板间距为d,电势差为U,板间电场可视为匀强电场;金属板下方有一磁感应强度为B的匀强磁场。带电量为+q、质量为m的粒子,由静止开始从正极板出发,经电场加速后射出,并进入磁场做匀速圆周运动。忽略重力的影响,求:
(1)粒子从电场射出时速度ν的大小;
(2)粒子在磁场中做匀速圆周运动的半径R。