已知首项为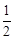 的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
的等比数列{an}是递减数列,其前n项和为Sn,且S1+a1,S2+a2,S3+a3成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)已知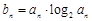 ,求数列{bn}的前n项和
,求数列{bn}的前n项和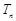 .
.
(本小题满分14分)
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC,F为CE上的点,且BF⊥平面ACE.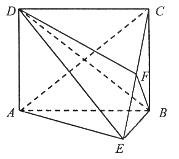
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD.
(本小题满分14分)
在△ABC中,AB=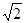 ,BC=1,
,BC=1,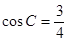 .
.
(1)求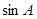 的值;(2)求
的值;(2)求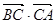 的值.
的值.
(本小题满分12分)设函数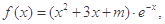 (其中
(其中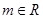 ,
,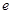 是自然对数的底数)
是自然对数的底数)
(I)若 处的切线方程;
处的切线方程;
(II)若函数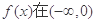 上有两个极值点.
上有两个极值点.
①实数m的范围;②证明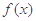 的极小值大于e.
的极小值大于e.
(本小题满分10分)已知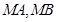 是曲线
是曲线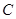 :
: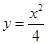 的两条切线,其中
的两条切线,其中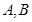 是切点,
是切点,
(I)求证: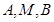 三点的横坐标成等差数列;
三点的横坐标成等差数列;
(II)若直线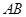 过曲线
过曲线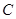 的焦点
的焦点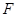 ,求
,求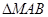 面积的最小值;
面积的最小值;
(本小题满分9分)平行四边形ABCD中,AB=2,AD=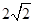 ,且
,且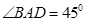 ,以BD为折线,把
,以BD为折线,把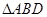 折起,使平面
折起,使平面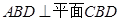 ,连AC.
,连AC.
(Ⅰ)求证: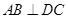 (Ⅱ)求二面角B-AC-D平面角的大小;
(Ⅱ)求二面角B-AC-D平面角的大小;
(Ⅲ)求四面体ABCD外接球的体积.