某商家推出一款简单电子游戏,弹射一次可以将三个相同的小球随机弹到一个正六边形的顶点与中心共七个点中的三个位置上(如图),用S表示这三个球为顶点的三角形的面积.规定:当三球共线时,S=0;当S最大时,中一等奖,当S最小时,中二等奖,其余情况不中奖,一次游戏只能弹射一次.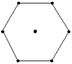
（1）求甲一次游戏中能中奖的概率;
（2）设这个正六边形的面积是6,求一次游戏中随机变量S的分布列及期望值.
（本小题满分13分）已知椭圆
的离心率为
，右焦点
到直线
的距离为
.
（Ⅰ）求椭圆C的方程；
（Ⅱ）过椭圆右焦点斜率为
的直线
与椭圆C相交于E、F两点，A为椭圆的右顶点，直线AE，AF分别交直线
于点M，N，线段MN的中点为P，记直线
的斜率为
，求证：
为定值.
（本小题满分13分）已知函数
（Ⅰ）当
时，求曲线
在点
处的切线方程；
（Ⅱ）当
时，讨论
的单调性.
（本小题满分12分）如图几何体中，四边形ABCD为矩形，
,G为FC的中点，M为线段CD上的一点，且
.
（Ⅰ）证明：AF//面BDG；
（Ⅱ）证明：面
面BFC；
（Ⅲ）求三棱锥
的体积V.
（本小题满分12分）设等差数列
的前
项和为
.数列
的前项和为
，且
.
（Ⅰ）求数列
的通项公式；
（Ⅱ）设
，求数列
的前项和
.
（本小题满分12分）参加市数学调研抽测的某高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏，但可见部分信息如下，据此解答如下问题：
（Ⅰ）求参加数学抽测的人数
、抽测成绩的中位数及分数分别在
，
内的人数；
（Ⅱ）若从分数在
内的学生中任选两人进行调研谈话，求恰好有一人分数在内的概率.