已知函数 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点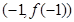 处的切线斜率为
处的切线斜率为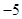 .
.
(1)求实数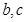 的值;
的值;
(2) 求函数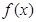 在区间
在区间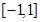 上的最小值;
上的最小值;
(Ⅲ)若函数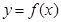 的图像上存在两点
的图像上存在两点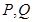 ,使得对于任意给定的正实数
,使得对于任意给定的正实数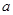 都满足
都满足 是以
是以 为直角顶点的直角三角形,且三角形斜边中点在
为直角顶点的直角三角形,且三角形斜边中点在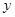 轴上,求点
轴上,求点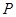 的横坐标的取值范围.
的横坐标的取值范围.
请考生在第22~24三题中任选一题作答,如果多做,则按所做的第一题记分.
(本小题满分10分)选修4-1:几何证明选讲
如图,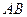 是⊙O的一条切线,切点为
是⊙O的一条切线,切点为 ,
,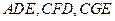 都是⊙O的割线,已知
都是⊙O的割线,已知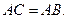 证明:
证明:
(Ⅰ)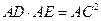 ;
;
(Ⅱ)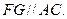
(本小题满分12分)
设 ,
,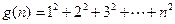 ,
,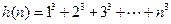 ,根据等差数列前n项和公式知
,根据等差数列前n项和公式知 ;且
;且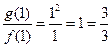 ,
, ,
, ,
,
猜想 ,即
,即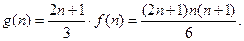
(Ⅰ)请根据以上方法推导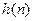 的公式;
的公式;
(Ⅱ)利用数学归纳法证明以上结论.
如图,已知四棱锥 的底面是正方形,
的底面是正方形,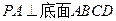 ,且
,且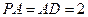 ,点
,点 分别在侧棱
分别在侧棱 、
、 上,且
上,且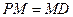 。
。
(Ⅰ)求证: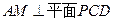 ;
;
(Ⅱ)若 ,求平面
,求平面 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.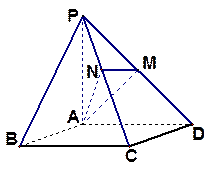
(本小题满分12分)
已知双曲线 的离心率为2,焦点到渐近线的距离等于
的离心率为2,焦点到渐近线的距离等于 ,过右焦点
,过右焦点 的直线
的直线
交双曲线于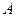 、
、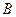 两点,
两点, 为左焦点.
为左焦点.
(Ⅰ)求双曲线的方程;
(Ⅱ)若 的面积等于
的面积等于 ,求直线
,求直线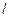 的方程.
的方程.
(本小题满分12分)
已知函数 在
在 和
和 处有极值。
处有极值。
(Ⅰ)求 的值;
的值;
(Ⅱ)求曲线 在
在 处的切线方程.
处的切线方程.