已知函数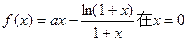
处取得极值.
（1）求实数a的值，并判断
上的单调性；
（2）若数列
满足
；
（3）在（2）的条件下，
记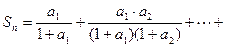
求证：
（本小题满分13分）在平面直角坐标系中，已知点
，点B在直线
：
上运动，过点B与垂直的直线和线段AB的垂直平分线相交于点M．
（1）求动点M的轨迹E的方程；
（2）过（1）中轨迹E上的点P (1,2)作两条直线分别与轨迹E相交于
，
两点．试探究：当直线PC，PD的斜率存在且倾斜角互补时，直线CD的斜率是否为定值？若是，求出这个定值；若不是，说明理由．
（本小题满分12分）已知等差数列
的首项
，前n项和为Sn，且
成等差数列．
（1）求数列
的通项公式；
（2）若数列{bn}为递增的等比数列，且集合
，设数列
的前n项和为
，求．
（本小题满分12分）设数列
的首项为1，前n项和为Sn，且
（
）．
（1）求数列
的通项公式；
（2）设
，
是数列
的前n项和，求
．
（本小题满分12分）在直三棱柱
中，
，
， 异面直线
与
所成的角等于
，设
．
（1）求a的值；
（2）求平面
与平面
所成的锐二面角的大小．
（本小题满分12分）已知a，b，c分别是△ABC的三个内角A，B，C所对的边，且
．
（1）求角C的值；
（2）若
，△ABC的面积
，求a的值．