如图，椭圆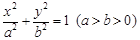
经过点
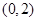，其左、右顶点分别是
、
，左、右焦点分别是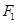
、
，
（异于、）是椭圆上的动点，连接
交直线
于
、
两点,若
成等比数列.
（Ⅰ）求此椭圆的离心率；
（Ⅱ）求证:以线段
为直径的圆过点.
如图，为处理含有某种杂质的污水，要制造一底宽为2米的无盖长方体沉淀箱，污水从
孔流入，经沉淀后从
孔流出，设箱体的长为
米，高为
米．已知流出的水中该杂质的质量分数与，的乘积
成反比，现有制箱材料60平方米，问当，各为多少米时，经沉淀后流出的水中该杂质的质量分数最小（，孔的面积忽略不计）．
已知函数
．
（1）若
，求函数
在
上的单调增区间；
（2）若函数在区间
上是单调递减函数，求实数
的取值范围．
已知
，
，复数
的虚部减去它的实部所得的差为
，求实数
．
已知数列1，11，111，1111，
，
，，写出该数列的一个通项公式，并用反证法证明该数列中每一项都不是完全平方数．
已知函数
，数列
满足
，
．
（1）求
；
（2）猜想数列的通项，并予以证明．