某家具厂生产一种儿童用组合床柜的固定成本为20000元，每生产一组该组合床柜需要增加投入100元，已知总收益满足函数：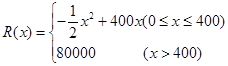
，其中
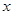是组合床柜的月产量.
（1）将利润
元表示为月产量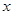组的函数；
（2）当月产量为何值时，该厂所获得利润最大？最大利润是多少？（总收益=总成本+利润）.
(12分) 已知平面区域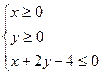
恰好被面积最小的圆C：
及其内部覆盖．
（1）求圆C的方程；
（2）斜率为1的直线
与圆C交于不同两点A、B，满足
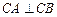，求直线的方程．
已知等差数列{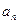
}中
．
（1）求数列{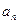}的通项公式；
（2）若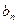
=
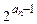，求数列
的前
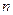项和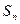
．
(12分) 已知关于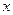
的一元二次不等式
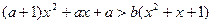对任意实数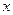都成立，试比较实数
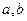的大小．
要设计一张矩形广告，该广告含有大小相等的左右两个矩形栏目（即图中阴影部分），这两栏的面积之和为18 000 cm2，四周空白的宽度为10 cm，两栏之间的中缝空白的宽度为5 cm，怎样确定广告的高与宽的尺寸（单位cm），能使矩形广告面积最小？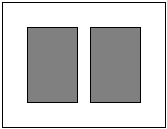
10分）已知圆C的圆心在直线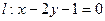
上，并且经过A（2，1）B（1，2）两点，求圆C的标准方程．