已知：如图，在平面直角坐标系中，一次函数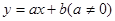
的图象与反比例函数
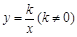的图象交于一、三象限内的A、B两点，与x轴交于C点，点A的坐标为(2，m)，点B的坐标为(n，
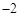），tan∠BOC
。
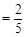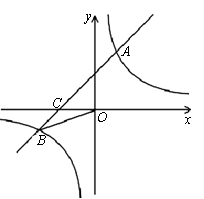
（l）求该反比例函数和一次函数的解析式；
（2）在x轴上有一点E（O点除外），使得△BCE与△BCO的面积相等，求出点E的坐标。
．如图，⊙O是△
的外接圆，
，
为⊙O的直径，且
，连结
．求BC的长．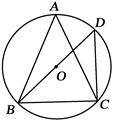 
用配方法将二次函数
化为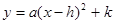
的形式（其中
为常数
），写出这个二次函数图象的顶点坐标 和对称轴方程，并在直角坐标系中画出他的示意图．
已知：如图，∠1=∠2，AB•AC=AD•AE.求证：∠C=∠E.
（本题6分）已知：如右图，在直径为10的⊙O中，做两条互相垂直的直径AE和BF，在弧EF上取点C，弦AC交BF于P，弦CB交AE于Q，求证：四边形APQB的面积等于25.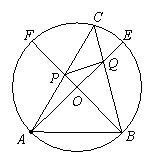
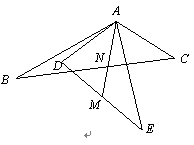
（本题10分）如右图，点A是△ABC和△ADE的公共顶点，∠BAC＋∠D
AE＝180°，AB＝AE，AC＝AD，点M是DE的中点，直线AM交直线BC于点N．将△ADE绕点A旋转，在旋转的过程中，请探究∠ANB与∠BAE的数量关系，并加以证明.