如图,平面 平面
平面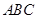 ,
,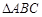 是等腰直角三角形,
是等腰直角三角形, ,四边形
,四边形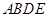 是直角梯形,
是直角梯形,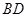 ∥AE,
∥AE,

 ,
, ,
,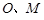 分别为
分别为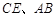 的中点.
的中点.
(1)求异面直线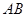 与
与 所成角的大小;
所成角的大小;
(2)求直线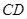 和平面
和平面 所成角的正弦值.
所成角的正弦值.
已知如图为函数f(x)=2sin(ωx+φ)(ω>0,0<φ<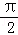 )的部分图象.
)的部分图象.
(1)求f(x)的解析式及其单调递增区间;
(2)求函数g(x)= 的值域.
的值域.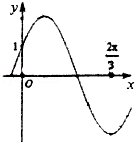
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],下图是按上述分组方法得到的频率分布直方图.
(1)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(2)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于l的概率.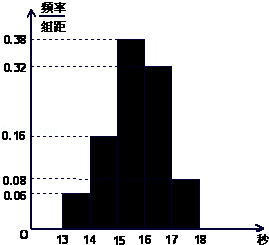
已知等比数列{an}满足:a1=2,a2•a4=a6.
(1)求数列{an}的通项公式;
(2)记数列bn=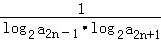 ,求该数列{bn}的前n项和Sn.
,求该数列{bn}的前n项和Sn.
设项数均为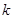 (
(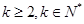 )的数列
)的数列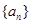 、
、 、
、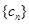 前
前 项的和分别为
项的和分别为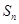 、
、 、
、 .已知
.已知 ,且集合
,且集合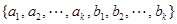 =
=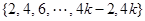 .
.
(1)已知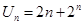 ,求数列
,求数列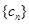 的通项公式;
的通项公式;
(2)若 ,求
,求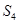 和
和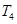 的值,并写出两对符合题意的数列
的值,并写出两对符合题意的数列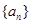 、
、 ;
;
(3)对于固定的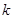 ,求证:符合条件的数列对(
,求证:符合条件的数列对(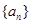 ,
, )有偶数对.
)有偶数对.
已知实数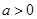 ,函数
,函数 .
.
(1)当 时,求
时,求 的最小值;
的最小值;
(2)当 时,判断
时,判断 的单调性,并说明理由;
的单调性,并说明理由;
(3)求实数 的范围,使得对于区间
的范围,使得对于区间 上的任意三个实数
上的任意三个实数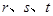 ,都存在以
,都存在以 为边长的三角形.
为边长的三角形.