(本题12分)在2008年北京奥运会青岛奥帆赛举行之前,为确保赛事安全,青岛海事部门举行奥运安保海上安全演习.为了测量正在海面匀速行驶的某航船的速度,在海岸上选取距离为1千米的两个观察点C,D,在某天10:00观察到该航船在A处,此时测得∠ADC=30°,3分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,求船的速度是多少千米/分钟.
如图在四棱锥 中,底面
中,底面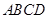 是矩形,
是矩形,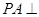 平面
平面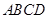 ,
,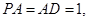
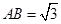 ,点
,点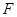 是
是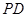 中点,点
中点,点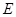 是
是 边上的任意一点.
边上的任意一点.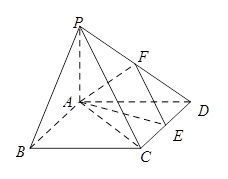
(1)当点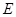 为
为 边的中点时,判断
边的中点时,判断 与平面
与平面 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)证明:无论点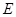 在
在 边的何处,都有
边的何处,都有 ;
;
(3)求三棱锥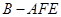 的体积.
的体积.
已知关于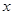 的一次函数
的一次函数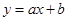
(1)设集合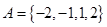 和
和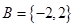 ,分别从集合
,分别从集合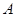 和
和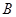 中随机取一个数作为
中随机取一个数作为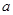 ,
,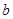 ,求函数
,求函数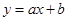 是增函数的概率;
是增函数的概率;
(2)若实数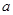 ,
,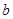 满足条件
满足条件 ,求函数
,求函数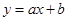 的图象不经过第四象限的概率.
的图象不经过第四象限的概率.
在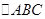 中,角
中,角 ,
, ,
, 所对的边分别为为
所对的边分别为为 ,
, ,
, ,且
,且
(1)求角 ;
;
(2)若 ,
, ,求
,求 ,
, 的值.
的值.
对任意实数列 ,定义
,定义 它的第
它的第 项为
项为
 ,假设
,假设 是首项是
是首项是 公比为
公比为 的等比数列.
的等比数列.
(1)求数列 的前
的前 项和
项和 ;
;
(2)若 ,
, ,
, .
.
①求实数列 的通项
的通项 ;
;
②证明: .
.
已知椭圆 的离心率
的离心率 ,长轴的左右端点分别为
,长轴的左右端点分别为 ,
, .
.
(1)求椭圆 的方程;
的方程;
(2)设动直线 与曲线
与曲线 有且只有一个公共点
有且只有一个公共点 ,且与直线
,且与直线 相交于点
相交于点 .问在
.问在 轴上是否存在定点
轴上是否存在定点 ,使得以
,使得以 为直径的圆恒过定点
为直径的圆恒过定点 ,若存在,求出
,若存在,求出 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.