为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
|
5 |
|
| 女生 |
10 |
|
|
| 合计 |
|
|
50 |
已知在全部50人中随机抽取1人,抽到喜爱打篮球的学生的概率为 .
.
(1)请将上表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理
由;下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)
已知数列 满足
满足 (
( 为常数,
为常数, ).
).
(Ⅰ)当 时,求
时,求 ;
;
(Ⅱ)当 时,求
时,求 的值;
的值;
(Ⅲ)问:使 恒成立的常数
恒成立的常数 是否存在?并证明你的结论.
是否存在?并证明你的结论.
某机床厂2011年年初用98万元购进一台数控机床,并立即投入生产使用.计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元;该机床使用后,每年的总收入为50万元.
设使用 年后数控机床的盈利额为
年后数控机床的盈利额为 万元.
万元.
(Ⅰ)写出 与
与 之间的函数关系式;
之间的函数关系式;
(Ⅱ)使用若干年后,对机床的处理方案有两种:
方案一:当年平均盈利额达到最大值时,以 万元价格处理该机床;
万元价格处理该机床;
方案二:当盈利额达到最大值时,以 万元价格处理该机床;
万元价格处理该机床;
请你研究一下哪种方案处理较为合理?并说明理由.
某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过 小时收费
小时收费 元,超过
元,超过 小时的部分每小时收费
小时的部分每小时收费 元(不足
元(不足 小时的部分按
小时的部分按 小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过
小时计算).现有甲、乙二人在该商区临时停车,两人停车都不超过 小时.
小时.
(Ⅰ)设甲停车付费a元.依据题意,填写下表:
| 甲停车时长 (小时) |
 |
 |
 |
 |
| 甲停车费a (元) |
(Ⅱ)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为 元的概率;
元的概率;
(Ⅲ)若甲停车 小时以上且不超过
小时以上且不超过 小时的概率为
小时的概率为 ,停车付费多于
,停车付费多于 元的概率为
元的概率为 ,求甲停车付费恰为
,求甲停车付费恰为 元的概率.
元的概率.
已知等差数列 满足:
满足: ,
, .
. 的前n项和为
的前n项和为 .
.
(Ⅰ)求 及
及 ;
;
(Ⅱ)令 (
( ),求数列
),求数列 的前n项和
的前n项和 .
.
设△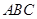 的内角
的内角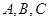 所对的边为
所对的边为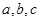 ,且有
,且有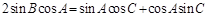 .
.
(Ⅰ)求角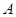 的大小;
的大小;
(Ⅱ)若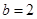 ,
,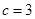 ,
,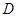 为
为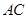 的中点,求
的中点,求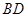 的长.
的长.