某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数:
①sin213°+cos217°-sin13°cos17°;
②sin215°+cos215°-sin15°cos15°;
③sin218°+cos212°-sin18°cos12°;
④sin2(-18°)+cos248°-sin(-18°)cos48°;
⑤sin2(-25°)+cos255°-sin(-25°)cos55°.
(1)试从上述五个式子中选择一个,求出这个常数;
(2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论.
(本小题满分12分)已知 在
在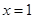 与
与 处都取得极值.
处都取得极值.
(1)求 ,
, 的值;
的值;
(2)设函数 ,若对任意的
,若对任意的 ,总存在
,总存在 ,使得
,使得 ,求实数
,求实数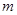 的取值范围.
的取值范围.
(本小题满分12分)数列 的前
的前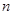 项和为
项和为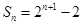 ,数列
,数列 是首项为
是首项为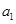 ,公差为
,公差为 (
( )的等差数列,且
)的等差数列,且 ,
,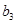 ,
,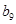 成等比数列.
成等比数列.
(1)求数列 与
与 的通项公式;
的通项公式;
(2)若 (
( ),求数列
),求数列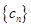 的前
的前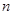 项和
项和 .
.
(本小题满分12分)已知函数 (
( )的导函数
)的导函数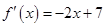 ,数列
,数列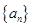 的前
的前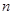 项和为
项和为 ,点
,点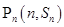 (
(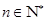 )均在函数
)均在函数 的图象上.
的图象上.
(1)求数列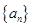 的通项公式;
的通项公式;
(2)求 的最大值.
的最大值.
(本小题满分12分)已知向量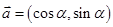 ,
,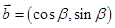 ,
, .
.
(1)求 的值;
的值;
(2)若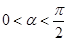 ,
,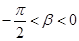 ,且
,且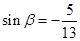 ,求
,求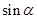 的值.
的值.
(本小题满分10分)已知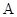 、
、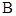 、
、 分别为
分别为 的三边
的三边 、
、 、
、 所对的角,向量
所对的角,向量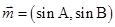 ,
,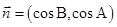 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,
, ,
,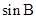 成等差数列,且
成等差数列,且 ,求边
,求边 的长.
的长.